高中数学合情推理和演绎推理选择题

如图所示，有三根针和套在一根针上的个金属片，按下列规则，把金属片从一根针上全部移到另一根针上。

（1）每次只能移动一个金属片；
（2）在每次移动过程中，每根针上较大的金属片不能放在较小的金属片上面。
若将个金属片从1号针移到3号针最少需要移动的次数记为，则=（   ）

A．33

B．31

C．17

D．15

下面几种推理中是演绎推理的序号为（  ）

A．半径为圆的面积，则单位圆的面积；

B．由金、银、铜、铁可导电，猜想：金属都可导电；

C．猜想数列的通项公式为；

D．由平面直角坐标系中圆的方程为，推测空间直角坐标系中球的方程为．

下列三句话按三段论的模式排列顺序正确的是（  ）
① 2013不能被2整除； ② 一切奇数都不能被2整除； ③ 2013是奇数；

A．①②③

B．②①③

C．②③①

D．③②①

把1,3,6,10,15,21，…这些数叫做三角形数，这是因为这些数目的点子可以排成一个正三角形，则第七个三角形数是(　 　)

A．21

B．28

C．32

D．36

用演绎法证明函数是增函数时的小前提是 （     ）

A．增函数的定义	B．函数满足增函数的定义
C．若，则	D．若，则

下列推理是归纳推理的是

A．A，B为定点，动点P满足|PA|＋|PB|＝2a＞|AB|，则P点的轨迹为椭圆

B．由a1＝1，an＝3n－1，求出S1，S2，S3，猜想出数列的前n项和Sn的表达式

C．由圆x^2＋y^2＝r^2的面积πr^2，猜想出椭圆＋＝1的面积S＝πab

D．科学家利用鱼的沉浮原理制造潜艇

把1、3、6、10、15、21、…这些数叫做三角形数，这是因为这些数目的点子可以排成一个正三角形(如图)，试求第七个三角形数是(　　)

A．27

B．28

C．29

D．30

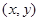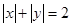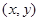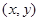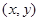观察下列事实：的不同整数解的个数为4 ，的不同整数解的个数为8，的不同整数解的个数为12，……，则的不同整数解的个数为（ ）

A．32

B．40

C．80

D．100

下列推理是归纳推理的是(　　)

A．A，B为定点，动点P满足|PA|＋|PB|＝2a>|AB|，则P点的轨迹为椭圆

B．由a1＝1，an＝3n－1，求出S1，S2，S3，猜想出数列的前n项和Sn的表达式

C．由圆x^2＋y^2＝r^2的面积πr^2，猜想出椭圆＝1的面积S＝πab

D．利用等差数列的性质推理得到等比数列的相关性质

平面上有个圆,其中每两个都相交于两点,每三个都无公共点,它们将平面分成块区域,有,则(   )

A．	B．
C．	D．

正弦函数是奇函数（大前提），是正弦函数（小前提），因此是奇函数（结论），以上推理（　　）

A．结论正确

B．大前提错误

C．小前提错误

D．以上都不对

命题：“正弦函数是奇函数，是正弦函数，因此是奇函数”结论是错误的，其原因是(   )　

A．大前提错误

B．小前提错误

C．推理形式错误

D．以上都不是

下面几种推理过程是演绎推理的是（     ）

A．由平面三角形的性质，推测空间四面体性质.

B．两条直线平行，同旁内角互补，如果和是两条平行直线的同旁内角，则.

C．某校高三共有10个班，1班51人，2班53人，3班52人，由此推测各班都超过50人.

D．在数列中，，由此归纳出的通项公式.

给出下面类比推理命题(其中Q为有理数集，R为实数集，C为复数集)：
①“若a，b∈R，则a－b＝0⇒a＝b”类比推出“若a，b∈C，则a－b＝0⇒a＝b”；
②“若a，b，c，d∈R，则复数a＋bi＝c＋di⇒a＝c，b＝d”类比推出“若a，b，c，d∈Q，则a＋b＝c＋d⇒a＝c，b＝d”；
③若“a，b∈R，则a－b>0⇒a>b”类比推出“若a，b∈C，则a－b>0⇒a>b”．
其中类比结论正确的个数是(    )

A．0

B．1

C．2

D．3

《论语•学路》篇中说：“名不正，则言不顺；言不顺，则事不成；事不成，则礼乐不兴；礼乐不兴，则刑罚不中；刑罚不中，则民无所措手足；所以，名不正，则民无所措手足．”上述推理用的是（   ）

A．一次三段论

B．复合三段论

C．不是三段论

D．某个部分是三段论