高中数学空间向量的应用试题

如图，四棱锥P-ABCD中，底面ABCD为平行四边形，PA⊥底面ABCD，M是棱PD的中点，且PA=AB=AC=2，．

（1）求证：CD⊥平面PAC；
（2）求二面角M-AB-C的大小；
（3）如果N是棱AB上一点，且直线CN与平面MAB所成角的正弦值为，求的值．

下列说法错误的是（ ）

A．两两相交且不过同一点的三条直线必在同一平面内；

B．过直线外一点有且只有一个平面与已知直线垂直；

C．如果共点的三条直线两两垂直，那么它们中每两条直线确定的平面也两两垂直；

D．如果两条直线和一个平面所成的角相等，则这两条直线一定平行．

下列说法错误的是（  ）

A．两两相交且不过同一点的三条直线必在同一平面内；

B．过直线外一点有且只有一个平面与已知直线垂直；

C．如果共点的三条直线两两垂直，那么它们中每两条直线确定的平面也两两垂直；

D．如果两条直线和一个平面所成的角相等，则这两条直线一定平行．

（本小题满分为10分）如图，将长为4，宽为1的长方形折叠成长方体ABCD-A₁B₁C₁D₁的四个侧面，记底面上一边，连接A₁B，A₁C，A₁D．

（1）当长方体ABCD-A₁B₁C₁D₁的体积最大时，求二面角B-A₁C-D的值；
（2）线段A₁C上是否存在一点P，使得A₁C平面BPD，若有，求出P点的位置，没有请说明理由．

如图，在多面体ABCDE中，DB⊥平面ABC，AE∥DB，且△ABC是边长为2的等边三角形，2AE＝BD＝2．

（Ⅰ）若F是线段CD的中点，证明：EF⊥面DBC；
（Ⅱ）求二面角D－EC－B的平面角的余弦值．

本小题满分12分）在平行六面体中，，,是的中点．

（1）证明：面;
（2）若，求直线与平面所成角的正弦值．

（本小题满分14分）如图，将一副三角板拼接，使他们有公共边BC，且使这两个三角形所在的平面互相垂直，，，，BC=6.

（1）证明：平面ADC^平面ADB；
（2）求B到平面ADC的距离.

设，是两条不同的直线，，是两个不同的平面，下列命题中正确的是（  ）

A．若，，，则

B．若，，且，则

C．若，，，则

D．若，，，则

如图, 是正方形， 平面，，  .

(Ⅰ) 求证：；
(Ⅱ) 求面FBE和面DBE所形成的锐二面角的余弦值.

（本小题满分14分）
在正三棱柱中，点是的中点，．
（1）求证：∥平面；
（2）试在棱上找一点，使．

（本小题满分13分）
如图，在正四面体中，分别是棱的中点.

（1）求证：四边形是平行四边形；
（2）求证：平面；
（3）求证：平面.

已知直线与平面，则下列四个命题中假命题是

A．如果，那么	B．如果，那么
C．如果，那么	D．如果，那么

设是两条不同的直线，是两个不同的平面，则下面四个命题中错误的是（    ）.

A．若，则//

B．若，则

C．若，则//或

D．若 //，则

如图，过四棱柱形木块上底面内的一点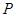和下底面的对角线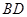将木块锯开，得到截面.

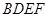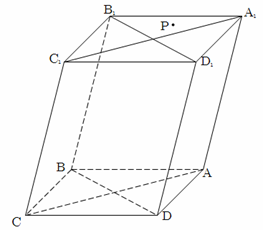
(1)请在木块的上表面作出过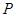的锯线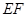，并说明理由；
(2)若该四棱柱的底面为菱形，四边形时矩形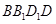，试证明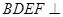：平面平面.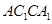

用,,表示空间中三条不同的直线, 表示平面, 给出下列命题:
① 若, , 则∥;  ② 若∥, ∥, 则∥;
③ 若∥, ∥, 则∥; ④ 若, , 则∥.
其中真命题的序号是（  ）

A．①②

B．②③

C．①④

D．②④