下列命题中假命题是( )
| A.垂直于同一条直线的两条直线相互垂直 |
| B.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 |
| C.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直 |
| D.若一个平面内的两条相交直线与另一个平面内的相交直线分别平行,那么这两个平面相互平行 |
(本小题满分12分)已知四棱锥 中,底面ABCD为直角梯形,BC//AD,
中,底面ABCD为直角梯形,BC//AD, ,且PA=AB=BC=1,AD=2,
,且PA=AB=BC=1,AD=2, 平面ABCD,E为AB的中点.
平面ABCD,E为AB的中点.
(Ⅰ)证明: ;
;
(Ⅱ)在线段PA上是否存在一点F,使EF//平面PCD,若存在,求 的值.
的值.
下列命题中,错误的是( )
| A.一条直线与两个平行平面中的一个相交,则必与另一个平面相交 |
| B.平行于同一平面的两条直线不一定平行 |
C.如果平面 不垂直于平面 不垂直于平面 ,那么平面 ,那么平面 内一定不存在直线垂直于平面 内一定不存在直线垂直于平面 |
D.若直线 不平行于平面 不平行于平面 ,则在平面 ,则在平面 内不存在与 内不存在与 平行的直线 平行的直线 |
(本小题满分12分)如图1,在Rt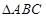 中,
中,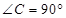 ,
,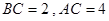 .
.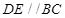 ,将
,将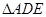 沿
沿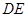 折起到
折起到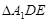 的位置,使
的位置,使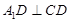 ,如图2.
,如图2.
(Ⅰ)求证: 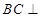 平面
平面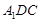 ;
;
(Ⅱ)若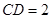 ,求平面
,求平面 与平面
与平面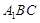 所成二面角的大小.
所成二面角的大小.
试题篮
()