用 ,
, ,
, 表示空间中三条不同的直线,
表示空间中三条不同的直线,  表示平面, 给出下列命题:
表示平面, 给出下列命题:
① 若 ,
,  , 则
, 则 ∥
∥ ; ② 若
; ② 若 ∥
∥ ,
,  ∥
∥ , 则
, 则 ∥
∥ ;
;
③ 若 ∥
∥ ,
,  ∥
∥ , 则
, 则 ∥
∥ ; ④ 若
; ④ 若

 ,
, 

 , 则
, 则 ∥
∥ .
.
其中真命题的序号是( )
| A.①② | B.②③ | C.①④ | D.②④ |
如图,定点 ,
, 都在平面
都在平面 内,定点
内,定点 ,
, ,
, 是
是 内异于
内异于 和
和 的动点,且
的动点,且 .那么,动点C在平面
.那么,动点C在平面 内的轨迹是( )
内的轨迹是( )
| A.一条线段,但要去掉两个点 | B.一个圆,但要去掉两个点 |
| C.一个椭圆,但要去掉两个点 | D.半圆,但要去掉两个点 |
(本小题满分12分)已知在四棱锥 中,底面
中,底面 是矩形,且
是矩形,且 ,
, ,
, 平面
平面 ,
, 、
、 分别是线段
分别是线段 、
、 的中点.
的中点.
(1)证明: ;
;
(2)判断并说明 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分14分)如图,在三棱锥P- ABC中,已知平面PBC  平面ABC.
平面ABC.
(1)若AB BC,CP
BC,CP PB,求证:CP
PB,求证:CP PA:
PA:
(2)若过点A作直线 ⊥平面ABC,求证:
⊥平面ABC,求证: //平面PBC.
//平面PBC.
(本小题满分14分)三棱柱 的直观图及三视图(正视图和俯视图是正方形,侧视图是等腰直角三角形)如图所示,
的直观图及三视图(正视图和俯视图是正方形,侧视图是等腰直角三角形)如图所示, 为
为 的中点.
的中点.

(1)求证: 平面
平面 ;
;
(2)求二面角 的正切值.
的正切值.
空间中,对于平面 和共面的两直线
和共面的两直线 、
、 ,下列命题中为真命题的是( ).
,下列命题中为真命题的是( ).
A.若 , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若 、 、 与 与 所成的角相等,则 所成的角相等,则 |
D.若 , , ,则 ,则 |
设l为直线,a,b是两个不同的平面,下列命题中正确的是
| A.若l//a,l//b,则a//b | B.若a//b,l//a,则l//b |
| C.若l^a,l//b,则a^b | D.若a^b,l//a,则l^b |
如图,在四棱锥 中,底面
中,底面 是菱形,且
是菱形,且 .
.
(1)求证: ;
;
(2)若平面 与平面
与平面 的交线为
的交线为 ,求证:
,求证: .
.
(本小题满分12分)在棱锥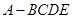 中,
中,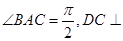 平面
平面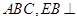 平面
平面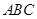 ,
,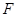 是
是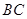 的中点,
的中点,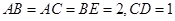
.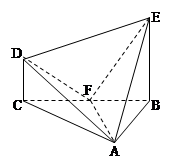
(1)求证: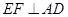 ;
;
(2)求三棱锥 的高。
的高。
如图,三角形 和梯形
和梯形 所在的平面互相垂直,
所在的平面互相垂直,  ,
, ,
, 是线段
是线段 上一点,
上一点, .
.
(Ⅰ)当 时,求证:
时,求证: 平面
平面 ;
;
(Ⅱ)求二面角 的正弦值;
的正弦值;
(Ⅲ)是否存在点 满足
满足 平面
平面 ?并说明理由.
?并说明理由.
如图,设P是60 的二面角
的二面角  内一点,PA
内一点,PA  平面
平面  ,PB
,PB  平面
平面  ,A、B为垂足若PA=4.PB=2,则AB的长为_______.
,A、B为垂足若PA=4.PB=2,则AB的长为_______.
如图所示,四棱锥P—ABCD中,AB AD,CD
AD,CD AD,PA
AD,PA 底面ABCD,PA=AD=CD=2AB=2,M为PC的中点。
底面ABCD,PA=AD=CD=2AB=2,M为PC的中点。
(1)求证:BM∥平面PAD;
(2)在侧面PAD内找一点N,使MN 平面PBD;
平面PBD;
(3)求直线PC与平面PBD所成角的正弦。
设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:
①m⊥α,n∥α,则m⊥n;
②若α γ=m,β
γ=m,β γ=n,m∥n ,则α∥β;
γ=n,m∥n ,则α∥β;
③若α∥β,β∥γ, m⊥α,则m⊥γ;
④若α⊥γ,β⊥γ,则α∥β.
其中正确命题的序号是 ( )
| A.①和③ | B.②和③ | C.③和④ | D.①和④ |
试题篮
()