高中数学空间向量的应用试题

下列命题中错误的是(     )

A．如果平面⊥平面，平面⊥平面，，那么

B．如果平面⊥平面，那么平面内一定存在直线平行于平面

C．如果平面不垂直于平面，那么平面内一定不存在直线垂直于平面

D．如果平面⊥平面，，过内任意一点作的垂线，则。

[2014·南通调研]设α，β是空间内两个不同的平面，m，n是平面α及β外的两条不同直线．从“①m⊥n；②α⊥β；③n⊥β；④m⊥α”中选取三个作为条件，余下一个作为结论，写出你认为正确的一个命题：________(用序号表示)．

[2012·安徽高考]设平面α与平面β相交于直线m，直线a在平面α内，直线b在平面β内，且b⊥m，则“α⊥β”是“a⊥b”的(　　)

A．充分不必要条件

B．必要不充分条件

C．充分必要条件

D．既不充分也不必要条件

[2013·南京模拟]已知l，m是两条不同的直线，α，β是两个不同的平面，下列命题：
①若l⊂α，m⊂α，l∥β，m∥β，则α∥β；
②若l⊂α，l∥β，α∩β＝m，则l∥m；
③若α∥β，l∥α，则l∥β；
④若l⊥α，m∥l，α∥β，则m⊥β.
其中真命题是________(写出所有真命题的序号)．

[2013·东城模拟]如图，在四面体ABCD中，若截面PQMN是正方形，则在下列命题中，错误的为(　　)

A．AC⊥BD

B．AC∥截面PQMN

C．AC＝BD

D．异面直线PM与BD所成的角为45°

如图，四棱锥中，底面为平行四边形，，，，是正三角形，平面平面．
（1）求证：；
（2）求三棱锥的体积．

如图，在四棱柱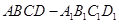中，底面ABCD和侧面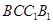都是矩形，E是CD的中点，，
.
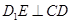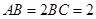（1）求证：；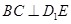
（2）若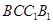平面与平面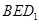所成的锐二面角的大小为，求线段的长度.

如图,在三棱锥 $P-ABC$中, $AB=AC,D$为 $BC$的中点, $PO\perp$平面 $ABC$,垂足 $O$落在线段 $AD$上,已知 $BC=8,PO=4,AO=3,OD=2$

（1）证明: $AP\perp BC$；

（2）在线段 $AP$上是否存在点 $M$,使得二面角 $A-MC-\beta$为直二面角？若存在,求出 $AM$的长;若不存在,请说明理由．

如图，已知四棱锥P—ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高，E为AD的中点．

(1)证明：PE⊥BC；
(2)若∠APB＝∠ADB＝60°，求直线PA与平面PEH所成角的正弦值．

如图所示，PA⊥⊙O所在的平面，AB是⊙O的直径，C是⊙O上的一点，E，F分别是点A在PB，PC上的射影，给出下列结论：①AF⊥PB；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC.其中正确结论的序号是________．

如图，在四棱锥中，，，，，，为线段上的点．
（Ⅰ）证明：；
（Ⅱ）若是的中点，求与所成的角的正切值；
（Ⅲ）若满足，求的值．

如图，四棱柱ABCD－A₁B₁C₁D₁的底面ABCD是正方形，O为底面中心，A₁O⊥平面ABCD，AB＝AA₁＝.

(1)证明：A₁C⊥平面BB₁D₁D；
(2)求平面OCB₁与平面BB₁D₁D的夹角θ的大小．

已知三棱锥中，，，直线与底面所成角为，则此时三棱锥外接球的表面积为（  ）

A．

B．

C．

D．

正方体ABCD﹣A₁B₁C₁D₁中，E为线段B₁D₁上的一个动点，则下列结论中错误的是（　　）

A．AC⊥BE

B．B1E∥平面ABCD

C．三棱锥E﹣ABC的体积为定值

D．直线B1E⊥直线BC1

菱形中，，且，现将三角形沿着折起形成四面体，如图所示.

（1）当为多大时，面？并证明；
（2）在（1）的条件下，求点到面的距离．