如图,已知 为平行四边形,
为平行四边形,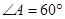 ,
,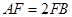 ,
, ,点
,点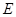 在
在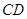 上,
上,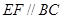 ,
,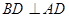 ,
,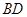 与
与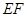 相交于
相交于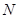 .现将四边形
.现将四边形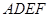 沿
沿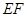 折起,使点
折起,使点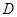 在平面
在平面 上的射影恰在直线
上的射影恰在直线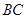 上.
上.
(1)求证: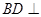 平面
平面 ;
;
(2)求折后直线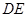 与平面
与平面 所成角的余弦值.
所成角的余弦值.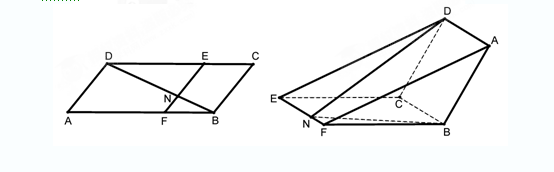
如图,在五面体 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, 平面
平面 ,
, ,
, ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正切值.
所成角的正切值.
如图,在四棱锥P-ABCD中,底面为直角梯形,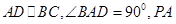 垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.
垂直于底面ABCD,PA=AD=AB=2BC=2,M,N分别为PC,PB的中点.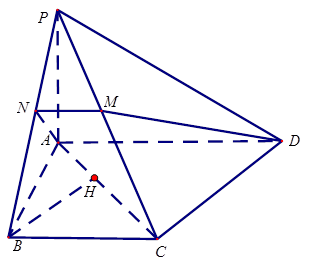
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求点B到平面PAC的距离.
如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点.
(1)求证:GH∥平面CDE;
(2)求证:面ADEF⊥面ABCD.
如图,在四面体 中,
中, ,
, ,点
,点 ,
, 分别是
分别是 ,
, 的中点.
的中点.
(1)EF∥平面ACD;
(2)求证:平面 ⊥平面
⊥平面 ;
;
(3)若平面 ⊥平面
⊥平面 ,且
,且 ,求三棱锥
,求三棱锥 的体积.
的体积.
如图,三棱柱ABC—A1B1C1的侧棱AA1⊥底面ABC,∠ACB = 90°,E是棱CC1上中点,F是AB中点,AC = 1,BC = 2,AA1 = 4.
(1)求证:CF∥平面AEB1;(2)求三棱锥C-AB1E的体积.
在如图所示的几何体中,四边形 是正方形,
是正方形, 平面
平面 ,
, ,
, 分别为
分别为 ,
, 的中点,且
的中点,且 .
.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求三棱锥 与四棱锥
与四棱锥 的体积之比.
的体积之比.
如图 ,在直角梯形
,在直角梯形 中,
中, ,
, ∥
∥ ,
, ,
, ,将
,将 沿
沿 折起,使平面
折起,使平面 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求几何体 的体积.
的体积.
如图所示,四棱锥 ,底面
,底面 是边长为
是边长为 的正方形,
的正方形, ⊥面
⊥面 ,
, ,过点
,过点 作
作 ,连接
,连接 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若面 交侧棱
交侧棱 于点
于点 ,求多面体
,求多面体 的体积.
的体积.
如图,直三棱柱 的侧棱长为3,
的侧棱长为3, ,且
,且 ,
, 、
、 分别是棱
分别是棱 、
、 上的动点,且
上的动点,且
(1)证明:无论 在何处,总有
在何处,总有 ;
;
(2)当三棱柱 .的体积取得最大值时,求异面直线
.的体积取得最大值时,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
试题篮
()