高中数学空间向量的应用解答题

如图，已知三角形△ABC与△BCD所在平面相互垂直，且∠BAC=∠BCD=90°，AB=AC，CB=CD，点P，Q分别在线段BD，CD上，沿直线PQ将△PQD向上翻折，使D与A重合．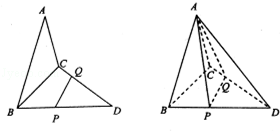

（Ⅰ）求证：AB⊥CQ；
（Ⅱ）求BP的长；
（Ⅲ）求直线AP与平面BCD所成的角．

如图所示的几何体中，四边形ABCD是等腰梯形，AB//CD， ，FC 平面ABCD， AE BD，CB =CD=-CF．
 
(Ⅰ)求证：平面ABCD 平面AED；
(Ⅱ)直线AF与面BDF所成角的余弦值

如图，在四棱锥中，底面是且边长为的菱形，侧面 是等边三角形，且平面⊥底面．

（1）若为的中点，求证：平面；
（2）求证：；
（3）求二面角的大小．

如图，在底面是直角梯形的四棱锥S-ABCD中，

(1)求四棱锥S-ABCD的体积;
(2)求证：
(3)求SC与底面ABCD所成角的正切值。

如图，ABCD是正方形，O是正方形的中心，PO底面ABCD，E是PC的中点。

求证：（1）PA∥平面BDE      
（2）平面PAC平面BDE

如图,平面平面,是以为斜边的等腰直角三角形,分别为,,的中点,,.
（1）设是的中点,证明:平面;
（2）证明:在内存在一点,使平面,并求点到,的距离.

如图1，在直角梯形中，，，且．现以为一边向形外作正方形，然后沿边将正方形翻折，使平面与平面垂直，为的中点，如图2．
（1）求证：∥平面；
（2）求证：平面；
（3）求点到平面的距离.

如图,在边长为1的等边三角形中,分别是边上的点,,是的中点,与交于点,将沿折起,得到如图5所示的三棱锥,其中.
(1) 证明://平面;
(2) 证明:平面;
(3) 当时,求三棱锥的体积.

在四棱锥中，底面为矩形，，，，，分别为的中点．
(1) 求证：；
(2) 求证：平面；

如图所示的长方体ABCD﹣A₁B₁C₁D₁中，底面ABCD是边长为2的正方形，O为AC与BD的交点，，M是线段B₁D₁的中点．
（1）求证：BM∥平面D₁AC；
（2）求证：D₁O⊥平面AB₁C；
（3）求二面角B﹣AB₁﹣C的大小．

如图，已知一四棱锥P－ABCD的底面是边长为1的正方形，且侧棱PC⊥底面ABCD，且PC＝2，E是侧棱PC上的动点
（1）求四棱锥P－ABCD的体积；
（2）证明：BD⊥AE。

 

如图所示，平面平面，且四边形为矩形，四边形为直角梯形，，，，．
（1）求证平面；（2）求平面与平面所成锐二面角的余弦值.

如图，在三棱锥中，，平面，,分别为,的中点.
（1）求证：平面；
（2）求证：平面平面.

如图，在三棱锥P—ABC中，D，E，F分别为棱PC，AC，AB的中点．已知PA⊥AC，PA=6，BC=8,DF=5.

求证：（1）直线PA∥平面DFE；
（2）平面BDE⊥平面ABC．

在如右图的几何体中，四边形为正方形，四边形为等腰梯形，∥，，，．
（1）求证：平面；
（2）求直线与平面所成角的正弦值．