高中数学空间向量的应用解答题

如图，已知四棱锥的底面为菱形，，，．

（Ⅰ）求证：；
（Ⅱ）求二面角的余弦值．

如图，在三棱锥S-ABC中，平面SAB⊥平面SBC，AB⊥BC，AS=AB，过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点．

求证：（1）平面EFG∥平面ABC．
（2）BC⊥SA．

（满分12分）如图，在直三棱柱中，∠ACB=90°；AC=BC=CC₁=2。

（1）求证：AB₁⊥BC₁；
（2）求点B到平面的距离；
（3）求二面角的大小。

如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，，，．

（Ⅰ）求证：平面PQB⊥平面PAD；
（Ⅱ）若二面角M﹣BQ﹣C为30°，设PM=tMC，试确定t的值．

（本小题满分12分）如图，在三棱柱中，面为矩形，，，为的中点，与交于点，面．

（Ⅰ）证明：；
（Ⅱ）若，求二面角的余弦值．

如图，斜三棱柱的底面是直角三角形，，点在底面内的射影恰好是的中点，且．

（1）求证：平面平面；
（2）若二面角的余弦值为，求斜三棱柱的侧棱 的长度．

如图，已知三棱柱的侧棱与底面垂直，且，，，，点、、分别为、、的中点．

（1）求证：平面；
（2）求证：面；

如图，已知四棱锥的底面为菱形，，，.

（Ⅰ）求证：；
（Ⅱ）求二面角的余弦值.

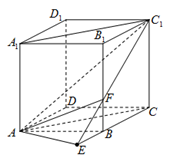
（本小题满分12分）如图，直四棱柱的底面是菱形，侧面是正方形，，是棱的延长线上一点，经过点、、的平面交棱于点，．

（1）求证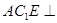：平面平面；
（2）求二面角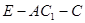的平面角的余弦值．

（本小题满分13分）如图，是圆的直径，是圆上异于的一个动点，垂直于圆所在的平面，DC∥EB，．

（1）求证：；
（2）当三棱锥C-ADE体积最大时，求平面AED与平面ABE所成的锐二面角的余弦值．

（本小题满分8分）如图，在四棱锥P−ABCD中，PD⊥底面ABCD，底面ABCD为平行四边形，∠ADB=90°，AB=2AD．

（Ⅰ）求证：平面PAD⊥平面PBD；
（Ⅱ）若PD=AD=1，，求二面角P−AD−E的余弦值．

（本小题满分14分）如图，平行四边形中，，，且，
正方形和平面成直二面角，是的中点．

（1）求证：．
（2）求证：平面．
（3）求三棱锥的体积．

（本小题满分12分）如图，在中，已知在上，且又平面．

（Ⅰ）求证：平面；
（Ⅱ）求证：⊥平面．

（本小题满分12分）如图，在中，已知在上，且又平面.

（Ⅰ）求证：⊥平面；
（Ⅱ）求二面角的余弦值．

（本小题满分12分）如图,四棱锥,侧面是边长为的正三角形,且与底面垂直,底面是的菱形,为的中点．

（Ⅰ）求证:；
（Ⅱ）求点到平面的距离．