已知命题p:∃x∈R,mx2+1≤0,命题q:∀x∈R,x2+mx+1>0,若p∧q为真命题,则实数m的取值范围是( )
| A.(-∞,-2) | B.[-2,0) |
| C.(-2,0) | D.(0,2) |
[2014·河南洛阳模拟]下列命题中的假命题是( )
| A.∀x∈R,2x-1>0 | B.∀x∈N*,(x-1)2>0 |
| C.∃x∈R,lgx<1 | D.∃x∈R,tanx=2 |
命题"对任意,都有
"的否定为( )
| A. |
存在
|
B. |
对任意
|
| C. |
存在
|
D. |
不存在
|
下列命题错误的是( )
A.命题“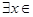 R使得 R使得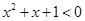 ”的否定是:“ ”的否定是:“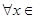 R均有 R均有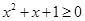 ”; ”; |
B.若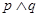 为假命题,则p,q均为假命题; 为假命题,则p,q均为假命题; |
C.若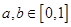 ,则不等式 ,则不等式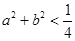 成立的概率是 成立的概率是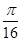 ; ; |
D.“平面向量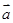 与 与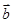 的夹角是钝角”的必要不充分条件是“ 的夹角是钝角”的必要不充分条件是“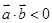 ”. ”. |
已知命题 “
“ ,有
,有 成立”,则
成立”,则 为( )
为( )
A. ,有 ,有 成立 成立 |
B. ,有 ,有 成立 成立 |
C. ,有 ,有 成立 成立 |
D. ,有 ,有 成立 成立 |
命题“对任意x∈R,都有x2≥0”的否定为( )
| A.存在x0∈R,使得x02<0 | B.对任意x∈R,使得x2<0 |
C.存在x0∈R,都有 |
D.不存在x∈R,使得x2<0 |
命题“对任意的x∈R,x3﹣x2+1≤0”的否定是( )
| A.不存在x∈R,x3﹣x2+1≤0 | B.存在x∈R,x3﹣x2+1≤0 |
| C.存在x∈R,x3﹣x2+1>0 | D.对任意的x∈R,x3﹣x2+1>0 |
命题“对任意x∈R,都有x2≥0”的否定为( )
| A.对任意x∈R,都有x2<0 | B.不存在x∈R,都有x2<0 |
| C.存在x0∈R,使得x02≥0 | D.存在x0∈R,使得x02<0 |
下列结论正确的是( )
A.若向量a∥b,则存在唯一的实数 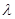 使 使 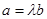 |
B.已知向量a,b为非零向量,则“a,b的夹角为钝角”的充要条件是“a b<0’’ b<0’’ |
C.“若 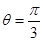 ,则 ,则 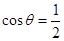 ”的否命题为“若 ”的否命题为“若 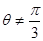 ,则 ,则 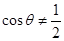 ” ” |
D.若命题 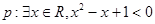 ,则 ,则 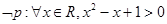 |
试题篮
()