高中数学二次剩余试题

当时，函数的最小值是_______，最大值是________。

二次函数的图像顶点为，且图像在x轴上截得线段长为8
（1）求函数的解析式；
（2）令  
①若函数在上是单调增函数，求实数的取值范围； 
②求函数在的最小值.

已知二次函数f（x）=ax²+bx+1的导函数 为f′（x），f′（0）＞0，f(x)与x轴恰有一个交点，则 的最小值为

A．

B．2

C．3

D．

已知函数的值域为，若关于x的不等式的解集为，则实数c的值为           ．

设二次函数的值域为，则的最小值为　　 　　．

不等式的整数解共有        个。

二次函数f(x)的二次项系数为正数，且对任意xÎR都有f(x)=f(4-x)成立，
若f(2－a²)<f(1+a－a²)，那么a的取值范围是                       (     )

A．1<a<2

B．a>1

C．a>2

D．a<1

二次函数f(x)的二次项系数为正数，且对任意xÎR都有f(x)=f(4-x)成立，
若f(2－a²)<f(1+a－a²)，那么a的取值范围是                        (     )

A．1<a<2

B．a>1

C．a>2

D．a<1

分解因式的结果是    ．

已知x₁、x₂是关于x的一元二次方程x²+（3a-1）x+2a²-1=0的两个实数根，使得
（3x₁-x₂）（x₁-3x₂）=-80成立．求实数a的所有可能值．

已知函数y＝ax²＋bx＋c的图象如图所示，则的值为(　　)

A．2b	B．a－b＋c
C．－2b	D．0

已知x₁、x₂是方程4x²-4mx+m+2=0的两个实根,当x₁²+x₂²取最小值时,实数m的值是（  ）

A．2

B．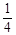

C．－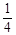

D．－1

若x≥0，y≥0，且，则的最小值是          。

设二次函数f(x)＝ax²－2ax＋c在区间[0,1]上单调递减，且f(m)≤f(0)，则实数m的取值范围是(　　)

A．(－∞，0]	B．[2，＋∞)
C．(－∞，0]∪[2，＋∞)	D．[0,2]

设，一元二次方程有整数根的充要条件是____________．