若函数f(x)=x2-ax-a在区间[0,2]上的最大值为1,则实数a等于( )
| A.-1 | B.1 | C.2 | D.-2 |
函数 满足
满足 ,且在区间
,且在区间 上的值域是
上的值域是 ,则坐标
,则坐标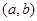 所表示的点在图中的( )
所表示的点在图中的( )
A.线段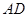 和线段 和线段 上 上 |
B.线段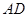 和线段 和线段 上 上 |
C.线段 和线段 和线段 上 上 |
D.线段 和线段 和线段 上 上 |
若函数y=ax与y=- 在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上( )
在(0,+∞)上都是减函数,则y=ax2+bx在(0,+∞)上( )
| A.单调递增 | B.单调递减 |
| C.先增后减 | D.先减后增 |
二次函数y=ax2+bx+c的图象如图2所示,则下列结论①abc<0,②b2-4ac>0,③2a+b>0,④a+b+c<0,⑤ x=0为方程ax2+bx+c=-2的一个解,其中正确的有 ( )

| A.2个 | B.3个 | C.4个 | D.5个 |
已知函数f(x)=ax2+bx+c,且a>b>c,a+b+c=0,则( )
| A.∀x∈(0,1),都有f(x)>0 |
| B.∀x∈(0,1),都有f(x)<0 |
| C.∃x0∈(0,1),使得f(x0)=0 |
| D.∃x0∈(0,1),使得f(x0)>0 |
试题篮
()