设二次函数 满足下列条件:
满足下列条件:
①当 时,
时,  的最小值为0,且
的最小值为0,且 恒成立;
恒成立;
②当 时,
时, 恒成立.
恒成立.
(I)求 的值;
的值;
(Ⅱ)求 的解析式;
的解析式;
(Ⅲ)求最大的实数m(m>1),使得存在实数t,只要当 时,就有
时,就有 成立
成立
(本小题满分12分)
已知函数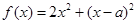 .
.
(Ⅰ)若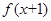 为偶函数,求
为偶函数,求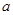 的值;
的值;
(Ⅱ)若 在
在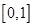 上有最小值9,求
上有最小值9,求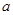 的值.
的值.
已知二次函数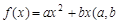 为常数,且
为常数,且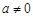 )满足条件:
)满足条件: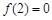 ,且方程
,且方程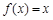 有两个相等的实数根.
有两个相等的实数根.
(1)求 的解析式;
的解析式;
(2)求函数在区间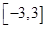 上的最大值和最小值;
上的最大值和最小值;
(3)是否存在实数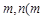
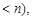 使
使 的定义域和值域分别为
的定义域和值域分别为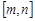 和
和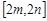 ,如果存在,求出
,如果存在,求出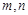 的值,如不存在,请说明理由.
的值,如不存在,请说明理由.
已知二次函数 的图象与
的图象与 轴有交点为
轴有交点为 ,
, 的图象与
的图象与 轴的交点为
轴的交点为 。设
。设 ,求证:
,求证: 的图象与
的图象与 轴的交点一定有一个介于点
轴的交点一定有一个介于点 与
与 之间。
之间。
(本小题满分12分)
已知二次函数 , 满足
, 满足 且
且 的最小值是
的最小值是 .(Ⅰ)求
.(Ⅰ)求 的解析式;(Ⅱ)设函数
的解析式;(Ⅱ)设函数 ,若函数
,若函数 在区间
在区间 上是单调函数,求实数
上是单调函数,求实数 的取值范围。
的取值范围。
(本小题满分14分)
二次函数 .
.
(1)若对任意
 有
有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)讨论函数 在区间
在区间 上的单调性;
上的单调性;
(3)若对任意的 ,
,
 有
有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知二次函数 的最小值为1,且
的最小值为1,且 。
。
(1)求 的解析式;
的解析式;
(2)若 在区间
在区间 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(3)在区间 上,
上, 的图象恒在
的图象恒在 的图象上方,试确定实数
的图象上方,试确定实数 的取值范围。
的取值范围。
试题篮
()