(本小题满分14分)函数f(x)=1-2a-2acosx-2sin2x的最小值为g(a)(a∈R).
(1)求g(a);
(2)若g(a)= ,求a及此时f(x)的最大值.
,求a及此时f(x)的最大值.
已知函数 ,若存在
,若存在 ,使
,使 ,则称
,则称 是函数
是函数 的一个不动点.设二次函数
的一个不动点.设二次函数 .
.
(1)对任意实数 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求 的取值范围;
的取值范围;
(2)在(1)的条件下,若 的图象上
的图象上 两点的横坐标是
两点的横坐标是 的不动点,且
的不动点,且 两点关于直线
两点关于直线 对称,求
对称,求 的最小值.
的最小值.
已知函数f(x)=a|x|+ (a>0,a≠1)
(a>0,a≠1)
(1)若a>1,且关于x的方程f(x)=m有两个不同的正数解,求实数m的取值范围;
(2)设函数g(x)=" f(" x),x∈[ 2,+∞), 满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
(本小题满分16分)某商品的市场需求量 (万件)、市场供应量
(万件)、市场供应量 (万件)与市场价格x(元/件)分别近似的满足下列关系:
(万件)与市场价格x(元/件)分别近似的满足下列关系: ,
, ,当
,当 时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量。
时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量。
(1)求平衡价格和平衡需求量;
(2)若要使平衡需求量增加6万件,政府对每件商品应给予多少元补贴?
(3)求当每件商品征税6元时新的平衡价格?
函数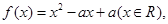 数列
数列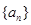 的前
的前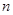 项和
项和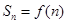 ,且
,且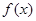 同时满足:①不等式
同时满足:①不等式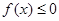 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在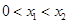 ,使得不等式
,使得不等式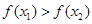 成立.
成立.
(1)求函数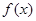 的表达式;
的表达式;
(2)求数列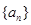 的通项公式.
的通项公式.
已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求a的取值范围
设二次函数 在区间
在区间 上的最大值、最小值分别是
上的最大值、最小值分别是 ,集合
,集合 .
.
(Ⅰ)若 ,且
,且 ,求
,求 的值;
的值;
(Ⅱ)若 ,且
,且 ,记
,记 ,求
,求 的最小值.
的最小值.
试题篮
()