高中数学二次剩余解答题

已知二次函数满足：,且的
解集为
（1）求的解析式；
（2）设,若在上的最小值为-4,求的值.

求证：二次函数的图象与轴交于的充要条件为．

已知函数.
(1)求不等式的解集;
(2)设,其中R,求在区间上的最小值.

已知中心在原点，焦点在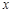轴上的椭圆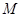的离心率为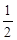，椭圆上异于长轴顶点的任意点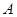与左右两焦点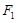、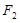构成的三角形中面积的最大值为.
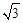（1）求椭圆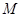的标准方程；
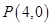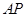（2）已知点，连接与椭圆的另一交点记为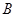，若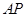与椭圆相切时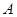、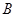不重合，连接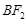与椭圆的另一交点记为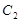，求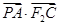的取值范围.

已知定义在区间[0,2]上的两个函数f(x)和g(x),其中f(x)=-x²+2ax+1+a²,g(x)=x-+.
(1)求函数f(x)的最小值.
(2)对于∀x₁,x₂∈[0,2],f(x₁)>g(x₂)恒成立,求实数a的取值范围.

已知二次函数的二次项系数为，且不等式的解集为（1，3）．
⑴若方程有两个相等实数根，求的解析式．
⑵若的最大值为正数，求实数的取值范围．

在△中，角所对的边分别为、、,若、是方程的两根，且;
（1）求角的大小；
（2）求边的长度；
（3）求的面积。

已知二次函数f(x)＝ax²＋bx＋c (a≠0)且满足f(－1)＝0，对任意实数x，恒有f(x)－x≥0，并且当x∈(0,2)时，f(x)≤.
(1)求f(1)的值；
(2)证明：a>0，c>0；
(3)当x∈[－1,1]时，函数g(x)＝f(x)－mx (x∈R)是单调函数，求证：m≤0或m≥1.

已知当x＝5时，二次函数f(x)＝ax²＋bx取得最小值，等差数列{a_n}的前n项和S_n＝f(n)，a₂＝－7.
(1)求数列{a_n}的通项公式；
(2)数列{b_n}的前n项和为T_n，且b_n＝，求T_n.

某通讯公司需要在三角形地带区域内建造甲、乙两种通信信号加强中转站，甲中转站建在区域内，乙中转站建在区域内．分界线固定，且=百米，边界线始终过点，边界线满足．
设()百米，百米.

(1)试将表示成的函数，并求出函数的解析式；
(2)当取何值时？整个中转站的占地面积最小，并求出其面积的最小值．

已知关于x的一元二次函数
(1)设集合P={1，2，3}和Q={－1，1，2，3，4}，分别从集合P和Q中随机取一个数作为和，
求函数在区间[上是增函数的概率；
(2)设点（，）是区域内的随机点，求函数上是增函数的概率.

二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.
（1）求f(x)的解析式；
（2）在区间[－1，1]上，y=f(x)的图象恒在y=2x+m的图象上方，求实数m的取值范围

已知二次函数f(x)＝ax²＋bx＋c图象的顶点为(－1，10)，且方程ax²＋bx＋c＝0的两根的平方和为12，求二次函数f(x)的表达式．

设y＝(log₂x)²＋(t－2)log₂x－t＋1，若t在[－2,2]上变化时，y恒取正值，求x的取值范围．

设函数(为实常数)为奇函数，函数().
(1)求的值；
(2)求在上的最大值；
(3)当时，对所有的及恒成立，求实数的取值范围．