高中数学二次剩余试题

函数f(x)=ax²－(2+a)x－3在区间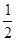［,1］是单调函数，则a的取值范围是　（　　）

A．0<a≤2	B．a≤2
C．a≥－2	D．a≥2

已知
⑴当不等式的解集为时，求实数的值；    
⑵若对任意实数，恒成立，求实数的取值范围；
⑶设为常数，解关于的不等式.

函数
（1）若f(-1)=0,并对恒有，求的表达式；
（2）在（1）的条件下，对，=—kx是单调函数，求k的范围。

函数
（1）若f(-1)=0,并对恒有，求的表达式；
（2）在（1）的条件下，对，=—kx是单调函数，求k的范围。

已知二次函数满足，且，
（1）求；
（2）求在上的最大值和最小值。

已知f(x)是定义域为R的偶函数，当x≥0时，f(x)＝x²－4x，那么，不等式f(x＋2)<5的解集是________．

已知，则函数的最小值是(    )

A．	B．
C．	D．

（本小题满分12分）
已知二次函数满足且
（1）求二次函数的解析式。
（2）在区间上，的图像恒在的图像的上方。
求实数m的取值范围。

．已知二次函数的图象经过点，是偶函数，函数的图象与直线相切，且切点位于第一象限
（Ⅰ）求函数的解析式
（Ⅱ）若对一切，不等式恒成立，求实数的取值范围
（Ⅲ）若关于x的方程有三个不同的实数解，求实数k的值

（1）设x、y、zR，且x＋y＋z＝1，求证x²＋y²＋z²≥；
（2）设二次函数f (x)＝ax²＋bx＋c（a＞0），方程f (x)－x＝0有两个实根x₁，x_2，
且满足：0＜x₁＜x₂＜，若x(0，x₁)。
求证：x＜f (x)＜x₁

若函数y＝x²－4x－2的定义域为[0，m]，值域为[－6，－2]，则m的取值范围是（   ）

A．(0，4)

B．[2，4]

C．(0，2)

D．(2，4)

的图象开口向上，且顶点在第二象限，则的图象大概是：

 

已知.

若a,b是非零向量，且，，则函数是

A．一次函数且是奇函数	B．一次函数但不是奇函数
C．二次函数且是偶函数	D．二次函数但不是偶函数

．关于的方程的两实根为，若，则的取值范围是（   ）

A．

B．

C．

D．