设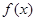 是定义在R上的偶函数,且在(-∞,0)上是增函数,则
是定义在R上的偶函数,且在(-∞,0)上是增函数,则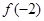 与
与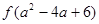
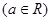 的大小关系是( )
的大小关系是( )
A.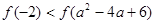 |
B.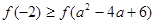 |
C.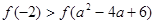 |
D.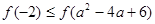 |
已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x).
(Ⅰ) 求函数f(x)的表达式;
(Ⅱ) 证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.
本题满分12分,每小题各4分)
已知函数 ,
,
(1)若函数 的值域为
的值域为 ,求实数a的值;
,求实数a的值;
(2)若函数 的递增区间为
的递增区间为 ,求实数a的值;
,求实数a的值;
(3)若函数 在区间
在区间
 上是增函数,求实数a的取值范围.
上是增函数,求实数a的取值范围.
已知函数 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当 时,
时, .
.
(1)现已画出函数 在y轴左侧的图象,如图所示,请补出完整函数
在y轴左侧的图象,如图所示,请补出完整函数 的图象,并根据图象写出函数
的图象,并根据图象写出函数 的增区间;
的增区间;
(2)求出函数 的解析式和值域.
的解析式和值域.
已知函数 的图象上一点
的图象上一点 ,过
,过 作平行于
作平行于 轴的直线
轴的直线 ,直线
,直线 ,求函数
,求函数 ,
, 和
和 轴,及直线
轴,及直线 轴围成的面积
轴围成的面积
已知函数f(x)=ax2+bx+c(a>0),α、β为方程f(x)=x的两根,且0<α<β< ,
,
0<x<α,给出下列不等式,其中成立的是 ( )
①x<f(x) ②α<f(x) ③x>f(x) ④α>f(x)
| A.①④ | B.③④ | C.①② |
D.②④ |
已知二次函数 的图象与x轴有两个不同的公共点,且
的图象与x轴有两个不同的公共点,且 ,当
,当 时,恒有
时,恒有 .
.
(1)当 时,求不等式
时,求不等式 的解集;
的解集;
(2)若以二次函数的图象与坐标轴的三个交点为顶点的三角形的面积为8,且 ,求a的值;
,求a的值;
(3)若 ,且
,且 对所有
对所有 恒成立,求正实数m的最小值.
恒成立,求正实数m的最小值.
已知二次函数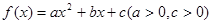 的图像与
的图像与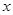 轴有两个不同的公共点,且有
轴有两个不同的公共点,且有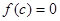 ,当
,当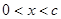 时,恒有
时,恒有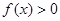 、
、
(1)试比较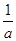 与c的大小;
与c的大小;
(2)试求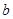 的取值范围;
的取值范围;
(3)若以二次函数的图像与坐标轴的三个交点为顶点的三角形的面积为5,求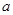 的取值范围
的取值范围
函数 的图象为曲线
的图象为曲线 ,函数
,函数 的图象为曲线
的图象为曲线 ,过
,过 轴上的动点
轴上的动点 作垂直于
作垂直于 轴的直线分别交曲线
轴的直线分别交曲线 ,
, 于
于 两点,则线段
两点,则线段 长度的最大值为( )
长度的最大值为( )
| A.2 | B.4 | C.5 | D. |
函数 满足
满足 ,且在区间
,且在区间 上的值域是
上的值域是 ,则坐标
,则坐标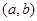 所表示的点在图中的( )
所表示的点在图中的( )
A.线段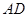 和线段 和线段 上 上 |
B.线段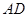 和线段 和线段 上 上 |
C.线段 和线段 和线段 上 上 |
D.线段 和线段 和线段 上 上 |
试题篮
()