设函数 对任意实数x 、y都有
对任意实数x 、y都有 ,
,
(1)求 的值;
的值;
(2)若 ,求
,求 、
、 、
、 的值;
的值;
(3)在(2)的条件下,猜想
 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。
把正整数排列成如图甲三角形数阵,然后擦去第偶数行中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,再把图乙中的数按从小到大的顺序排成一列,得到一个数列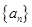 ,若
,若 ,则
,则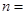 ________.
________.
设函数f(x)= (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)= , f2(x)=f(f1(x))=
, f2(x)=f(f1(x))=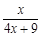 , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))=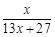 , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))= ……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
用 个不同的实数
个不同的实数 可得
可得 个不同的排列,每个排列为一行写成一个
个不同的排列,每个排列为一行写成一个 行的矩阵,
行的矩阵,
对第 行
行 ,记
,记 ,(
,( ),例如由1、2、3
),例如由1、2、3
排数阵知:由于此数阵中每一列各数之和都是12,所以 ,那
,那
么由1,2,3,4,5形成的数阵中, ( )
( )
| A.—3600 | B.1800 | C.—1080 | D.—720 |
用数学归纳法证明1+ <n,其中n>1且n∈N*,在验证n=2时,式子的左边等于________.
<n,其中n>1且n∈N*,在验证n=2时,式子的左边等于________.
下列推理中属于归纳推理且结论正确的是( )
| A.由an=2n﹣1,求出S1=12,S2=22,S3=32,…,推断:数列{an}的前n项和Sn=n2 |
B.由f(x)=xcosx满足f(﹣x)=﹣f(x)对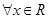 都成立,推断:f(x)=xcosx为奇函数 都成立,推断:f(x)=xcosx为奇函数 |
C.由圆x2+y2=r2的面积S=πr2,推断:椭圆 =1的面积S=πab =1的面积S=πab |
D.由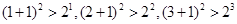 ,…,推断:对一切 ,…,推断:对一切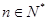 ,(n+1)2>2n ,(n+1)2>2n |
试题篮
()