高中数学第二数学归纳法试题

观察下面的算式：
根据以上规律，把（为自然数且）写成这种和式形式，和式中最大的数为           ．

用数学归纳法证明等式时，第一步验证时，左边应取的项是（***）

A．1

B．

C．

D．

设函数对任意实数x 、y都有，
（1）求的值；
（2）若，求、、的值；
（3）在（2）的条件下，猜想的表达式，并用数学归纳法加以证明。

（本小题满分10分）已知数列中，，
（Ⅰ）求；（Ⅱ）猜想的表达式，并用数学归纳法加以证明.

某个命题与正整数n有关,若n=k(k∈N^*)时命题成立,那么可推得当n=k+1时该命题也成立,现已知n=5时,该命题不成立,那么可以推得

A．n=6时该命题不成立	B．n=6时该命题成立
C．n=4时该命题不成立	D．n=4时该命题成立

数列满足，前n项和
　（1）写出；（2）猜出的表达式，并用数学归纳法证明

用数学归纳法证明“”验证n=1成立时,左边所得项是（  ）                                       

A．

B．

C．

D．

比较与的大小

是否存在常数a、b、c，使等式对一切正整数n都成立？证明你的结论

用数学归纳法证明
时，由的假设到证明时，等式左边应添加的式子是       ．

16、用数学归纳法证明等式时,当时左边表达式是       ;从需增添的项的是                 。

用数学归纳法证明：

是否存在实数使得关于n的等式
成立？若存在，求出的值并证明等式，若不存在，请说明理由.

用数学归纳法证明：，第二步证明“从到”，左端增加的项数是（   ）

A．

B．

C．

D．

设函数f（x）＝（x＞0），观察：f₁（x）＝f（x）＝, f₂（x）＝f（f₁（x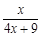））＝, f₃（x）＝f（f₂（x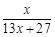））＝, f₄（x）＝f（f₃（x））＝……根据以上事实，由归纳推理可得：当n∈N*, n≥2时，f_n（x）＝f（_n－1（x））＝             ．