高中数学第二数学归纳法试题

已知数列{a_n}，{b_n}满足a₁=，a_n+b_n=1，b_n+1=，则b₂₀₁₁=（ ）

A．

B．

C．

D．

在用数学归纳法证明f（n）=++…+＜1（n∈N^*，n≥3）的过程中：假设当n=k（k∈N^*，k≥3）时，不等式f（k）＜1成立，则需证当n=k+1时，f（k+1）＜1也成立．若f（k+1）=f（k）+g（k），则g（k）=（ ）

A．+

B．+﹣

C．﹣

D．﹣

用数学归纳法证明1+2+3+…+n³=，则当n=k+1时，左端应在n=k的基础上加上（ ）

A．k^3+1

B．（k+1）^3

C．

D．（k^3+1）+（k^3+2）+（k^3+3）+…+（k^3+1）^3

若a₁≤a₂≤…≤a_n，而b₁≥b₂≥…≥b_n或a₁≥a₂≥…≥a_n而b₁≤b₂≤…≤b_n，证明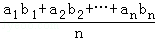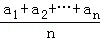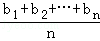：≤（）•（）．当且仅当a₁=a₂=…=a_n或b₁=b₂=…=b_n时等号成立．

用数学归纳法证明等式时，写出到时左边应增加的项为？

观察下列各式：，，，，，…，则_______．

已知任意一个正整数的三次幂可表示成一些连续奇数的和，如图所示，可表示为，则我们把7、9、11叫做的“数因子”，若的一个“数因子”为，则       

已知任意一个正整数的三次幂可表示成一些连续奇数的和，如图所示，可表示为，则我们把7、9、11叫做的“数因子”，若的一个“数因子”为，则       

（1）用数学归纳法证明等式1+2+3+…+（n+3）= ．
（2）用数学归纳法证明不等式．

用数学归纳法证明“4^2n-1＋3ⁿ⁺¹（n∈N^*）能被13整除”的第二步中，当n=k＋1时为了使用归纳假设，对4^2k+1＋3^k+2变形正确的是（   ）

A．16（4^2k-1＋3^k+1）-13×3^k+1

B．4×4^2k＋9×3^k

C．（4^2k-1＋3^k+1）＋15×4^2k-1＋2×3^k+1

D．3（4^2k-1＋3^k+1）-13×4^2k-1

用数学归纳法证明1²+2²+…+（n﹣1）²+n²+（n﹣1）²+…+2²+1²═时，由n=k的假设到证明n=k+1时，等式左边应添加的式子是（ ）

A．（k+1）^2+2k^2	B．（k+1）^2+k^2
C．（k+1）^2	D．

观察下列各不等式：




…
（1）由上述不等式，归纳出一个与正整数有关的一般性结论；
（2）用数学归纳法证明你得到的结论．

观察下列等式
                                     第一个式子
                              第二个式子
                      第三个式子
               第四个式子
照此规律下去
（Ⅰ）写出第个等式；
（Ⅱ）你能做出什么一般性的猜想？请用数学归纳法证明猜想． 

在数列{a_n}中，a₁＝，a_n＋1＝，求a₂、a₃、a₄的值，由此猜想数列{a_n}的通项公式，并用数学归纳法证明你的猜想．

数列满足．
（1）计算，，，，并由此猜想通项公式；
（2）用数学归纳法证明（1）中的猜想．