高中数学第二数学归纳法试题

　已知数列的前和为，其中且
(1)求
(2)猜想数列的通项公式，并用数学归纳法加以证明．

观察下列式子  , … … ,则可归纳出_______.

当时，

(1)求,,,；
(2)猜想与的关系，并用数学归纳法证明．

用数学归纳法证明“对于的自然数都成立”时，第一步证明中的起始值应取_____________．

（本小题满分12分）证明：能够被6整除.

用数学归纳法证明： 

利用数学归纳法证明   时，从“”变到“”时，左边应增乘的因式是

A．

B．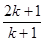

C．

D．

用数学归纳法证明不等式“”时的过程中，由到时，不等式的左边（    ）

A．增加了一项

B．增加了两项

C．增加了两项，又减少了；

D．增加了一项，又减少了一项；

如图，在圆内画条线段，将圆分割成两部分；画条相交线段，彼此分割成条线段，将圆分割成部分；画条线段，彼此最多分割成条线段，将圆最多分割成部分；画条线段，彼此最多分割成条线段，将圆最多分割成部分.
       
（1）猜想：圆内两两相交的条线段，彼此最多分割成多少条线段？
（2）记在圆内画条线段，将圆最多分割成部分，归纳出与的关系.
（3）猜想数列的通项公式，根据与的关系及数列的知识，证明你的猜想是否成立.

用数学归纳法证明等式时,当时左边表达式是       ;从需增添的项的是                 .

用数学归纳法证明：

用数学归纳法证明“(n＋1)(n＋2)·…·(n＋n)＝2ⁿ·1·3·…·(2n－1)”，从“k到k＋1”左端需增乘的代数式为(　  )

A．2k＋1

B．2(2k＋1)

C．

D．

（本小题满分12分）
由下列不等式：，，，，，你能得到一个怎样的一般不等式？并加以证明．

用数学归纳法证明“”（）时，从“”时，左边应增添的式子是

A．

B．

C．

D．

本题理科做.
设，（、）。
（1）求出的值；
（2）求证：数列的各项均为奇数.