高中数学第二数学归纳法试题

已知，则，， ，逐个求出，， ，由以上计算结果进行归纳推理，可得           .

已知f（n）＝1＋＋＋…＋ （n∈N^*），用数学归纳法证明时，等于________．

如图所示，∠AOB=1rad，点Al，A2， 在OA上，点B1，B2， 在OB上，其中的每一个实线段和虚线段的长均为1个长度单位，一个动点M从O点出发，沿着实线段和以O为圆心的圆弧匀速运动，速度为l长度单位／秒，则质点M到达A₃点处所需要的时间为  秒，质点M到达An点处所需要的时间为  秒．

一种平面分形图的形成过程如下图所示，第一层是同一点出发的三条线段，长度均为1，每两条线段夹角为 120°；第二层是在第一层的每一条线段末端，再生成两条与该线段成120°角的线段，长度不变；第三层按第二层的方法再在第二层每一条线段的末端各生成两条线段；重复前面的作法，直至第6层，则分形图第6层各条线段末端之间的距离的最大值      

在数列{a_n}中，a₁＝，a_n＋1＝，求a₂、a₃、a₄的值，由此猜想数列{a_n}的通项公式，并用数学归纳法证明你的猜想．

观察下列等式
                                     第一个式子
                              第二个式子
                      第三个式子
               第四个式子
照此规律下去
（Ⅰ）写出第个等式；
（Ⅱ）你能做出什么一般性的猜想？请用数学归纳法证明猜想． 

正偶数列有一个有趣的现象：①；②；
③
按照这样的规律，则2012在第              个等式中。

观察下列各不等式：




…
（1）由上述不等式，归纳出一个与正整数有关的一般性结论；
（2）用数学归纳法证明你得到的结论．

观察下列等式：，，，， ，由以上等式推测出一个一般性的结论：对于N^*，___________．

设函数对任意实数x 、y都有，
（1）求的值；
（2）若，求、、的值；
（3）在（2）的条件下，猜想的表达式，并用数学归纳法加以证明。

有下列各式：，，，……
则按此规律可猜想此类不等式的一般形式为：                        ．

已知 ，定义，．经计算…，照此规律，则          ．

（本题14分）某少数民族的刺绣有着悠久的历史，下图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都由小正方形构成，小正方形数越多刺绣越漂亮，现按同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含个小正方形.

（Ⅰ）求出；
（Ⅱ）利用合情推理的“归纳推理思想”归纳出与的关系式，
（Ⅲ）根据你得到的关系式求的表达式.

已知下列四个等式


依此类推，猜想第个等式为                                                    ．

【原创】
（1）观察下列各式;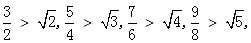根据以上各式利用归纳推理得出一个一般性的结论；
（2）设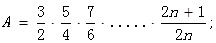根据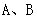的大小关系证明（1）的结论；