高中数学三面角、直三面角的基本性质试题

已知函数，则=      .

．．（本小题满分14分）定义在上的函数，如果满足；对任意，存在常数，都有成立，则称是上的有界函数，其中称为函数的上界.已知函数.
（Ⅰ）当时，求函数在上的值域，并判断函数在上是否为有界函数，请说明理由；
（Ⅱ）若是上的有界函数，且的上界为3，求实数的取值范围；
（Ⅲ）若，求函数在上的上界的取值范围.

．（本小题满分13分）汽车和自行车分别从地和地同时开出，如下图，各沿箭头方向（两方向垂直）匀速前进，汽车和自行车的速度分别是10米/秒和5米/秒，已知米.（汽车开到地即停止）

（Ⅰ）经过秒后，汽车到达处，自行车到达处，设间距离为，试
写出关于的函数关系式，并求其定义域.
（Ⅱ）经过多少时间后，汽车和自行车之间的距离最短？最短距离是多少？

（13分，理科做）已知函数的定义域为，且同时满足：①；②恒成立；③若，则有．
（1）试求函数的最大值和最小值；
（2）试比较与的大小N）；
（3）某人发现：当x=(nÎN)时，有f(x)<2x＋2.由此他提出猜想：对一切xÎ(0,1,都有，请你判断此猜想是否正确，并说明理由．

若任取x_1，x₂∈[a，b]，且x₁≠x₂，都有成立，则称f(x)[a，b]上的凸函数。试问：在下列图像中，是凸函数图像的为

A                 B                   C                  D

已知函数的图像经过（o，1），且
（1）求的值域；
（2）设命题，命题q：函数在R上无极值，是否存在实数m满足复合命题p且q为真命题？若存在，求出m的范围；若不存在，说明理由．

下列函数中，满足“对任意，，当时，”的是

A．

B．

C．

D．

预测人口的变化趋势有多种方法，“直接推算法”使用的公式是，其中Pn为预测人口数，P0为初期人口数，k为预测年内增长率，n为预测期间隔年数．如果在某一时期有-1<k<0，那么这期间人口数   （   ）

A．呈上升趋势

B．呈下降趋势

C．摆动变化

D．不变

已知函数，，记.
（1）若，且在上恒成立，求实数的取值范围；
（2）若，且存在单调递减区间，求的取值范围；
（3）若，设函数的图象与函数图象交于点、，过线段的中点作轴的垂线分别交，于点、，请判断在点处的切线与在点处的切线能否平行，并说明你的理由.

本小题满分12分）设函数，当点是函数图象上的点时，点是函数图象上的点．
（1）写出函数的解析式；
（2）若当时，恒有，试确定的取值范围；
（3）把的图象向左平移个单位得到的图象，函数，（）在的最大值为，求的值

．（本小题满分14分）甲乙两人连续年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图：

甲调查表明：每个鱼池平均产量从第年万只鳗鱼上升到第年万只。
乙调查表明：全县鱼池总个数由第年个减少到第年个。
（1）求第年全县鱼池的个数及全县出产的鳗鱼总数；
（2）哪一年的规模(即总产量)最大?请说明理由.

、(本小题满分12分)已知函数
（1）若，求的零点；
（2）若函数在区间上有两个不同的零点，求的取值范围。

（本小题满分12分）某投资商到一开发区投资72万元建起了一座蔬菜加工厂，经营中，第一年支出12万元，以后每年支出增加4万元，从第一年起每年蔬菜销售收入50万元.设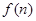表示前n年的纯利润总和，（f（n）=前n年的总收入–前n年的总支出–投资额72万元）.
（I）该厂从第几年开始盈利？
（II）该厂第几年年平均纯利润达到最大？并求出年平均纯利润的最大值.

设Q为有理数集，函数f (x) = g(x)=，则函数h(x)= f (x)·g(x)

A．是奇函数但不是偶函数	B．是偶函数但不是奇函数
C．既是奇函数也是偶函数	D．既不是偶函数也不是奇函数

已知a=2^0.2，b=0.4^0.2，c=0.4^0.6，则

A．a>b>c

B．a>c>b

C．c>a>b

D．b>c> a