若函数 ,
, 同时满足下列条件,
同时满足下列条件,
(1) 在D内为单调函数;(2)存在实数m,n.当 时,
时, ,则称此函数为D内等射函数,设
,则称此函数为D内等射函数,设
 则:①
则:① 在
在 的单调性为 ;②当
的单调性为 ;②当 为R内的等射函数时,
为R内的等射函数时, 的取值范围是 .
的取值范围是 .
(本小题满分12分)
某单位建造一间地面面积为12 平方米的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过 米 ,房屋正面的造价为400元/平方米,房屋侧面的造价为150元/平方米,屋顶和地面的造价费用合计为5800元,如果墙高为3米,且不计房屋背面的费用.(1)把房屋总造价y表示成x的函数,并写出该函数的定义域;(2)当侧面的长度为多少时,总造价最低?最低造价是多少?
米 ,房屋正面的造价为400元/平方米,房屋侧面的造价为150元/平方米,屋顶和地面的造价费用合计为5800元,如果墙高为3米,且不计房屋背面的费用.(1)把房屋总造价y表示成x的函数,并写出该函数的定义域;(2)当侧面的长度为多少时,总造价最低?最低造价是多少?
(本小题满分14分)已知函数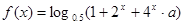 ;
;
(1)若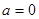 ,求
,求 的值域;(2)在(1)的条件下,判断
的值域;(2)在(1)的条件下,判断 的单调性;(3)当
的单调性;(3)当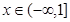 时
时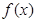 有意义求实
有意义求实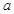 的范围。
的范围。
有10台型号相同的联合收割机,收割一片土地上的庄稼.现有两种工作方案:第一种方案,同时投入并连续工作至收割完毕;第二种方案,每隔相同时间先后投入,每一台投入后都连续工作至收割完毕.若采用第一种方案需要24小时,而采用第二种方案时,第一台投入工作的时间恰好为最后一台投入工作时间的5倍,则采用第二种方案时第一台收割机投入工作的时间为 小时.
(本小题满分14分)如图所示,某市政府决定在以政府大楼O为中心、正北方向
和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考
虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正
面要朝市政府大楼.设扇形的半径OM=R , ,OB与OM之间的夹角为
,OB与OM之间的夹角为 .
.
(1)将图书馆底面矩形ABCD的面积S表示成 的函数.
的函数.
(2)若 R=45 m,求当 为何值时,矩形ABCD的面积S有最大值?
为何值时,矩形ABCD的面积S有最大值?
其最大值是多少?
(本小题满分14分)
在△ABC中,BC=2,AB+AC=3,中线AD的长为y,AB的长为x,
(1) 建立y与x的函数关系式,并指出其定义域.
(2) 求y的最小值,并指出x的值.
已知 是二次方程
是二次方程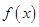 的两个不同实根,
的两个不同实根, 是二次方程
是二次方程 的两个不同实根,若
的两个不同实根,若 ,则 ( )
,则 ( )
A.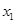 , , 介于 介于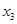 和 和 之间 之间 |
B.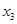 , , 介于 介于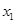 和 和 之间 之间 |
C.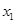 与 与 相邻, 相邻,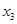 与 与 相邻 相邻 |
D.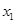 , , 与 与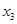 , , 相间相列 相间相列 |
一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的长、宽分别为x、y,剪去部分的面积为20,若2≤x≤10,记y=f(x),则y=f(x)的图象是( )

试题篮
()