高中数学三面角、直三面角的基本性质试题

本题共有3个小题，第1小题满分5分，第2小题满分6分,
第3小题满分7分.
对定义在区间上的函数，若存在闭区间和常数，使得对任意的都有，且对任意的都有恒成立，则称函数为区间上的“U型”函数。
（1）求证：函数是上的“U型”函数；
（2）设是（1）中的“U型”函数，若不等式对一切的恒成立，
求实数的取值范围；
（3）若函数是区间上的“U型”函数，求实数和的值.

如图所示：矩形的一边在轴上，另两个顶点在函数的图像上（其中点的坐标为），矩形的面积记为，则="           "

已知的值为          

若是R上的奇函数，且当时，，则的反函数的图像大致是（   ）

函数y＝f(x)(x∈R)的图象如下图所示，则函数g(x)＝f(log_ax)(0<a<1)的单调减区间是(　　)

（本小题满分12分）设函数，（且）。
(1)设，判断的奇偶性并证明；
(2)若关于的方程有两个不等实根，求实数的范围；
(3)若且在时，恒成立，求实数的范围。

已知函数是定义在R上的奇函数，当时，，则不等式的解集是

A．

B．

C．

D．

.（本小题满分12分）
已知函数是定义在实数集R上的奇函数，当＞0时，
（1）已知函数的解析式；
（2）若函数在区间上是单调减函数，求a的取值范围；
（3）试证明对.

（本小题满分12分）
某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池，池的深度一定（平面图如图所示），如果池四周围墙建造单价为400元/米，中间两道隔墙建造单价为248元/米，池底建造单价为80元/米²，水池所有墙的厚度忽略不计.
（1）试设计污水处理池的长和宽，使总造价最低，并求出最低总造价；
（2）若由于地形限制，该池的长和宽都不能超过16米，试设计污水池的长和宽，使总造价最低.

已知两个正数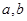,可按规则扩充为一个新数,在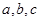三个数中取两个较大的数,按上述规则扩充得到一个新数，依次下去，将每扩充一次得到一个新数称为一次操作.
（1）若,按上述规则操作三次,扩充所得的数是__________；
（2）若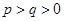，经过6次操作后扩充所得的数为（为正整数），则的值分别为____________

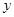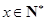某公司购买一批机器投入生产，据市场分析每台机器生产的产品可获得的总利润（万元）与机器运转时间（年数，）的关系为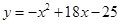.则当每台机器运转    年时，年平均利润最大，最大值是    万元.

方程3x²－e^x=0的实根    (     )

A．不存在

B．有一个

C．有二个

D．有三个

已知则等于           （   ）

A．

B．

C．

D．

方程X－1＝lgX必有一个根的区间是(     )

A．(0. 1, 0. 2)

B．(0. 2, 0. 3)

C．(0. 3, 0. 4)

D．(0. 4, 0. 5)

如图，要设计一张矩形广告，该广告含有大小相等的左右两个矩形栏目（即图中阴影部分），这两栏的面积之和为18000，四周空白的宽度为10，两栏之间的中缝空白的宽度为5，怎样确定广告的高与宽的尺寸（单位：），能使矩形广告面积最小？