高中数学选择题

已知 $F_1$ ， $F_2$ 是椭圆 $C：\mathit{\hspace{0.33em}\hspace{0.33em}}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\hspace{0.33em}(a>b>0)$ 的左，右焦点， $A$ 是 $C$ 的左顶点，点 $P$ 在过 $A$ 且斜率为 $\frac{\sqrt{3}}{6}$ 的直线上， $△P{F}_1{F}_2$ 为等腰三角形， $\angle F_1{F}_{2}P=120°$ ，则 $C$ 的离心率为（    ）

A．

$\frac{2}{3}$

B．

$\frac{1}{2}$

C．

$\frac{1}{3}$

D．

$\frac{1}{4}$

已知 $f\left(x\right)$ 是定义域为 $(-\infty ,+\infty )$ 的奇函数,满足 $f(1-x)=f(1+x)$ .若 $f\left(1\right)=2$ ，则 $f\left(1\right)+f\left(2\right)+f\left(3\right)+\cdots +f\left(50\right)=$ （    ）

A．

$-50$

B．

$0$

C．

$2$

D．

$50$

若 $f\left(x\right)=\text{cos}x-\text{sin}x$ 在 $\left[-a,\mathit{\hspace{0.33em}a}\right]$ 是减函数，则 $a$ 的最大值是（    ）

A．

$\frac{\pi }{4}$

B．

$\frac{\pi }{2}$

C．

$\frac{3\pi }{4}$

D．

$\pi$

在长方体 $\mathit{ABCD}-A_1{B}_1{C}_1{D}_1$ 中， $\mathit{AB}=\mathit{BC}=1$ ， $A{A}_1=\sqrt{3}$ ，则异面直线 $A{D}_1$ 与 $D{B}_1$ 所成角的余弦值为（    ）

A．

$\frac{1}{5}$

B．

$\frac{\sqrt{5}}{6}$

C．

$\frac{\sqrt{5}}{5}$

D．

$\frac{\sqrt{2}}{2}$

设 $a={\mathit{log}}_{0.2}0.3$ ， $b={\mathit{log}}_{2}0.3$ ，则(   )

A．	$a+b<\mathit{ab}<0$	B．	$\mathit{ab}<a+b<0$
C．	$a+b<0<\mathit{ab}$	D．	$\mathit{ab}<0<a+b$

设 $F_1$ , $F_2$ 是双曲线 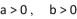（ ）的左、右焦点， $O$ 是坐标原点．过 $F_2$ 作 $C$ 的一条渐近线的垂线，垂足为 $P$ ．若 $\left|P{F}_1\right|=\sqrt{6}\left|\mathit{OP}\right|$ ，则 $C$ 的离心率为(   )

A．

$\sqrt{5}$

B．

$\sqrt{3}$

C．

$2$

D．

$\sqrt{2}$

$△\mathit{ABC}$ 的内角 $\mathit{A\hspace{0.33em}}，\mathit{\hspace{0.33em}\hspace{0.33em}B\hspace{0.33em}}，\mathit{\hspace{0.33em}\hspace{0.33em}C}$ 的对边分别为 $a$ ， $b$ ， $c$ ，若 $△\mathit{ABC}$ 的面积为 $\frac{a^2+b^2-c^2}{4}$ ，则 $C=$ (   )

A．

$\frac{\pi }{2}$

B．

$\frac{\pi }{3}$

C．

$\frac{\pi }{4}$

D．

$\frac{\pi }{6}$

某群体中的每位成员使用移动支付的概率都为 $p$ ，各成员的支付方式相互独立，设 $X$ 为该群体的10位成员中使用移动支付的人数， $\mathit{DX}=2.4$ ， $P\left(X=4\right)<P\left(X=6\right)$ ，则 $p=$ (   )

A．

0.7

B．

0.6

C．

0.4

D．

0.3

函数 $y=-x^4+x^2+2$ 的图像大致为(   )

A．		B．
C．		D．

直线 $x+y+2=0$ 分别与 $x$ 轴， $y$ 轴交于 $A$ ， $B$ 两点，点 $P$ 在圆 ${\left(x-2\right)}^2+y^2=2$ 上，则 $△\mathit{ABP}$ 面积的取值范围是(   )

A．

$\left[2\hspace{0.33em}，\mathit{\hspace{0.33em}\hspace{0.33em}}6\right]$

B．

$\left[4\hspace{0.33em}，\mathit{\hspace{0.33em}\hspace{0.33em}}8\right]$

C．

$\left[\sqrt{2}\hspace{0.33em}，\mathit{\hspace{0.33em}\hspace{0.33em}}3\sqrt{2}\right]$

D．

$\left[2\sqrt{2}\hspace{0.33em}，\mathit{\hspace{0.33em}\hspace{0.33em}}3\sqrt{2}\right]$

已知 成等比数列，且 $a_1+a_2+a_3+a_4=\mathit{ln}(a_1+a_2+a_3)$ ．若 ，则（    ）

A．

$a_1<a_3,a_2<a_4$

B．

$a_1>a_3,a_2<a_4$

C．

$a_1<a_3,a_2>a_4$

D．

$a_1>a_3,a_2>a_4$

已知 $\stackrel{⃑}{a}$ 、 $\stackrel{⃑}{b}$ 、 $\stackrel{⃑}{e}$ 是平面向量， $\stackrel{⃑}{e}$ 是单位向量．若非零向量 $\stackrel{⃑}{a}$ 与 $\stackrel{⃑}{e}$ 的夹角为 $\frac{\pi }{3}$ ，向量 $\stackrel{⃑}{b}$ 满足 ${\stackrel{⃑}{b}}^2-4\stackrel{⃑}{e}\cdot \stackrel{⃑}{b}+3=0$ ，则 $\left|\stackrel{⃑}{a}-\stackrel{⃑}{b}\right|$ 的最小值是（    ）

A．

$\sqrt{3}-1$

B．

$\sqrt{3}+1$

C．

2

D．

$2-\sqrt{3}$

已知四棱锥 $S-\mathit{ABCD}$ 的底面是正方形，侧棱长均相等， $E$ 是线段 $\mathit{AB}$ 上的点（不含端点），设 $\mathit{SE}$ 与 $\mathit{BC}$ 所成的角为 ${\theta }_1$ ， $\mathit{SE}$ 与平面 $\mathit{ABCD}$ 所成的角为 ${\theta }_2$ ，二面角 $S-\mathit{AB}-C$ 的平面角为 ${\theta }_3$ ，则（    ）

A．

${\theta }_1\le {\theta }_2\le {\theta }_3$

B．

${\theta }_3\le {\theta }_2\le {\theta }_1$

C．

${\theta }_1\le {\theta }_3\le {\theta }_2$

D．

${\theta }_2\le {\theta }_3\le {\theta }_1$

设 $0<p<1$ ，随机变量 $\xi$ 的分布列如图，则当 $p$ 在 $\left(0,1\right)$ 内增大时，（    ）

$\xi$	$0$	$1$	$2$
$P$	$\frac{1-p}{2}$	$\frac{1}{2}$	$\frac{p}{2}$

A．	$D\left(\xi \right)$ 减小	B．	$D\left(\xi \right)$ 增大
C．	$D\left(\xi \right)$ 先减小后增大	D．	$D\left(\xi \right)$ 先增大后减小

设函数 $f\left(x\right)=\left\{\begin{array}{c}{2}^{-x}，x\le 0\\ 1，x>0\end{array}\right.$ ，则满足 $f\left(x+1\right)<f\left(2x\right)$ 的 x的取值范围是（ ）

A．

$(-\infty ,-1]$

B．

$\left(0，+\infty \right)$

C．

$\left(-1，0\right)$

D．

$\left(-\infty ，0\right)$