高中数学解答题

在中，角，，所对的边分别是，，，且满足
（1）求角的大小；
（2）设，求的最大值，并求取得最大值时，的值.

(本小题满分10分)选修4-5：不等式选讲
设函数，其中，
（1）当时，求不等式的解集
（2）若不等式的解集为，求的值.

（本小题满分10）选修4－1：几何证明选讲
如图，过圆O外一点M作它的一条切线，切点为A，过A作直线AP垂直直线OM，垂足为P.
（1）证明：；
（2）N为线段AP上一点，直线NB垂直直线ON，且交圆O于B点。过B点的切
线交直线ON于K。证明：∠OKM = 90°.

（本小题满分12分）
设，数列满足，，求：
（1）数列的通项公式；
（2）证明：对一切正整数，.

（本小题满分12分）已知函数（），其中．
（Ⅰ）当时，讨论函数的单调性；
（Ⅱ）若函数仅在处有极值，求的取值范围；
（Ⅲ）若对于任意的，不等式在上恒成立，求的取值范围．

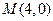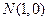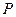（本小题满分12分）已知，，若动点满足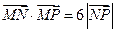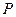，点的轨迹为曲线.
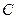（Ⅰ）求曲线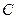的方程；
（Ⅱ）试确定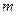的取值范围，使得对于直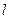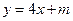线：，曲线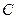上总有不同的两点关于直线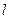对称.

（本小题满分12分）已知是边长为的正方形的中心，点、分别是、的中点，沿对角线把正方形折成直二面角；

（Ⅰ）求的大小；
（Ⅱ）求二面角的余弦值；
（Ⅲ）求点到面的距离.

（本小题满分12分）设命题：集合是集合的子集；命题：函数在上是增函数，若为真命题，为假命题，求实数的取值范围.

已知四棱锥P-ABCD，底面ABCD是、边长为的菱形，又，且PD=CD，点M、N分别是棱AD、PC的中点．
（1）证明：DN//平面PMB；
（2）求DN与MB所成的角的正弦值．

已知函数，且 ， 的定义域为区间
，
（1）求的解析式；
（2）判断的增减性.

正四棱台的上、下底边长为4m和6m．
（1）若侧面与底面所成的角是60°,求此四棱台的表面积；
（2）若侧棱与底面所成的角是60°,求此四棱台的体积.

P为椭圆上一点，、为左右焦点，若
（1）   求△的面积；
（2）   求P点的坐标．

.求证：△ABC是等边三角形的充要条件是，这里是的三条边。

．已知程序框图为：指出其功能（用算式表示）

（ 10分）已知双曲线的左、右焦点分别为，，过点的动直线与双曲线相交于两点．
（I）若动点满足（其中为坐标原点），求点的轨迹方程；
（II）在轴上是否存在定点，使·为常数？若存在，求出点的坐标；
若不存在，请说明理由．