高中数学解答题

已知矩阵的逆矩阵,求矩阵的特征值.

设.
(Ⅰ)求的最大值及最小正周期；
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,锐角A满足,，求的值.

如图，在四棱锥中，底面是矩形，分别为的中点，，且

（1）证明：；
（2）求二面角的余弦值。

已知在时有极大值6，在时有极小值，求a，b，c的值；并求区间上的最大值和最小值.

如图，在正方体中，是的中点.

（1）求证：平面；
（2）求证：平面平面.

已知抛物线的焦点为F₂，点F₁与F₂关于坐标原点对称，直线m垂直于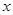轴（垂足为T），与抛物线交于不同的两点P、Q，且.
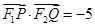（Ⅰ）求点T的横坐标；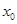
（Ⅱ）若椭圆C以F₁,F₂为焦点，且F₁,F₂及椭圆短轴的一个端点围成的三角形面积为1.
① 求椭圆C的标准方程；
② 过点F₂作直线l与椭圆C交于A,B两点，设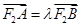，若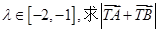的取值范围.

已知函数 ．
（Ⅰ）若a>0，函数y=f(x)在区间(a，a ²-3)上存在极值，求a的取值范围；
（Ⅱ）若a>2，求证：函数y=f(x)在(0，2)上恰有一个零点．

设为等差数列，为数列的前项和，已知.
（Ⅰ）求数列的通项公式；
（Ⅱ）设，求数列的前项和.

函数 ()的部分图像如图所示.

（Ⅰ）求函数的解析式；
（Ⅱ）中，角的对边分别为，若，
其中，且，求角的大小.

已知函数，．
（Ⅰ）若函数，求的取值范围；
（Ⅱ）若不等式有解，求的取值范围．

曲线的参数方程为（为参数），将曲线上所有点的横坐标伸长为原来的2倍，纵坐标伸长为原来的倍，得到曲线.
（Ⅰ）求曲线的普通方程；
（Ⅱ）已知点，曲线与轴负半轴交于点，为曲线上任意一点， 求
的最大值.

如图, ⊙O为的外接圆，直线为⊙O的切线，切点为，直线∥，交于，交⊙O于，为上一点，且.

求证：（Ⅰ）；
（Ⅱ）点、、、共圆.

已知函数.
（Ⅰ）若在处取得极值，求实数的值；
（Ⅱ）若恒成立，求实数的取值范围.

如图，已知椭圆的中心在原点，其上、下顶点分别为，点在直线上，点到椭圆的左焦点的距离为.

（Ⅰ）求椭圆的标准方程；
（Ⅱ）设是椭圆上异于的任意一点，点在轴上的射影为，为的中点，直线交直线于点，为的中点，试探究：在椭圆上运动时，直线与圆:的位置关系，并证明你的结论.

2012年伦敦奥运会前夕，在海滨城市青岛举行了一场奥运选拔赛，其中甲、乙两名运动员为争取最后一个参赛名额进行了7轮比赛,得分的情况如茎叶图所示（单位：分）.

甲		乙
8	7	9
5 4 5 4 1	8	4 4 6 7 4
1	9	1

（Ⅰ）分别求甲、乙两名运动员比赛成绩的平均分与方差；
（Ⅱ）若从甲运动员的7轮比赛的得分中任选3个不低于80分且不高于90分的得分，求这3个得分与其平均分的差的绝对值都不超过2的概率.