已知抛物线 的准线与x轴交于点M,过点M作圆
的准线与x轴交于点M,过点M作圆 的两条切线,切点为A、B,
的两条切线,切点为A、B, .
.
(1)求抛物线E的方程;
(2)过抛物线E上的点N作圆C的两条切线,切点分别为P、Q,若P,Q,O(O为原点)三点共线,求点N的坐标.
定义在[﹣1,1]上的奇函数f(x)满足f(1)=2,且当a,b∈[﹣1,1],a+b≠0时,有 .
.
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若 对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
设函数 的定义域为E,值域为F.
的定义域为E,值域为F.
(1)若E={1,2},判断实数λ=lg22+lg2lg5+lg5﹣ 与集合F的关系;
与集合F的关系;
(2)若E={1,2,a},F={0,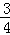 },求实数a的值.
},求实数a的值.
(3)若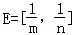 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值.
定义在[﹣1,1]上的奇函数f(x)满足f(1)=2,且当a,b∈[﹣1,1],a+b≠0时,有 .
.
(1)试问函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标;若不存在,请说明理由并加以证明.
(2)若 对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
已知定点
 与分别在
与分别在 轴、
轴、 轴上的动点
轴上的动点 满足:
满足: ,动点
,动点 满足
满足 .
.
(1)求动点 的轨迹的方程;
的轨迹的方程;
(2)设过点 任作一直线与点
任作一直线与点 的轨迹交于
的轨迹交于 两点,直线
两点,直线 与直线
与直线 分别交于点
分别交于点 (
( 为坐标原点);
为坐标原点);
(i)试判断直线 与以
与以 为直径的圆的位置关系;
为直径的圆的位置关系;
(ii)探究 是否为定值?并证明你的结论.
是否为定值?并证明你的结论.
如图已知抛物线 :
: 过点
过点 ,直线
,直线 交
交 于
于 ,
, 两点,过点
两点,过点 且平行于
且平行于 轴的直线分别与直线
轴的直线分别与直线 和
和 轴相交于点
轴相交于点 ,
, .
.
(1)求 的值;
的值;
(2)是否存在定点 ,当直线
,当直线 过点
过点 时,△
时,△ 与△
与△ 的面积相等?若存在,求出点
的面积相等?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知数列 中,
中,
(1)求 ,
, ;
;
(2)求证: 是等比数列,并求
是等比数列,并求 的通项公式
的通项公式 ;
;
(3)数列 满足
满足 ,数列
,数列 的前n项和为
的前n项和为 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知数列{an}的各项均为正数的等比数列,且a1a2=2,a3a4=32,
(1)求数列{an}的通项公式;
(2)设数列{bn}满足 (n∈N*),求设数列{bn}的前n项和Tn.
(n∈N*),求设数列{bn}的前n项和Tn.
已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)证明:对任意的 ,存在唯一的
,存在唯一的 ,使
,使 ;
;
(3)设(2)中所确定的 关于
关于 的函数为
的函数为 ,证明:当
,证明:当 时,有
时,有 .
.
如图,点 是椭圆
是椭圆 的一个顶点,
的一个顶点, 的长轴是圆
的长轴是圆 的直径,
的直径, 、
、 是过点
是过点 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中 交圆
交圆 于
于 、
、 两点,
两点, 交椭圆
交椭圆 于另一点
于另一点 .
.
(1)求椭圆 的方程;
的方程;
(2)求 面积的最大值及取得最大值时直线
面积的最大值及取得最大值时直线 的方程.
的方程.
已知等差数列 的首项
的首项 ,公差
,公差 ,且
,且 、
、 、
、 分别是等比数列
分别是等比数列 的
的 、
、 、
、 .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设数列 对任意正整数
对任意正整数 均有
均有 成立,求
成立,求 的值.
的值.
已知点 在抛物线
在抛物线 上,直线
上,直线 (
( ,且
,且 )与抛物线
)与抛物线 ,相交于
,相交于 、
、 两点,直线
两点,直线 、
、 分别交直线
分别交直线 于点
于点 、
、 .
.
(1)求 的值;
的值;
(2)若 ,求直线
,求直线 的方程;
的方程;
(3)试判断以线段 为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
为直径的圆是否恒过两个定点?若是,求这两个定点的坐标;若不是,说明理由.
已知函数 ,
, .
.
(1)若函数 在其定义域上为增函数,求
在其定义域上为增函数,求 的取值范围;
的取值范围;
(2)当 时,函数
时,函数 在区间
在区间 上存在极值,求
上存在极值,求 的最大值.
的最大值.
(参考数值:自然对数的底数 ≈
≈ ).
).
已知抛物线C:
 ,点A、B在抛物线C上.
,点A、B在抛物线C上.
(1)若直线AB过点M(2p,0),且 =4p,求过A,B,O(O为坐标原点)三点的圆的方程;
=4p,求过A,B,O(O为坐标原点)三点的圆的方程;
(2)设直线OA、OB的倾斜角分别为 ,且
,且 ,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由.
,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由.
已知函数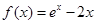 ,
,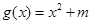 (
( )
)
(1)对于函数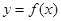 中的任意实数x,在
中的任意实数x,在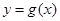 上总存在实数
上总存在实数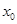 ,使得
,使得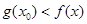 成立,求实数
成立,求实数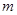 的取值范围
的取值范围
(2)设函数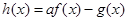 ,当
,当 在区间
在区间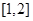 内变化时,
内变化时,
(1)求函数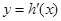
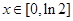 的取值范围;
的取值范围;
(2)若函数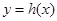
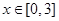 有零点,求实数m的最大值.
有零点,求实数m的最大值.
试题篮
()