[选修4-5:不等式选讲]
已知函数 .
(1)当 时,求不等式 的解集;
(2)若不等式 的解集包含 ,求 a的取值范围.
[选修4―4:坐标系与参数方程]
在直角坐标系 中,曲线 C的参数方程为 ,直线 l的参数方程为 .
(1)若 ,求 C与 l的交点坐标;
(2)若 C上的点到 l的距离的最大值为 ,求a.
已知椭圆C: ,四点P1(1,1),P2(0,1),P3 ,P4 中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布 .
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在 之外的零件数,求 及 的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 |
10.12 |
9.96 |
9.96 |
10.01 |
9.92 |
9.98 |
10.04 |
10.26 |
9.91 |
10.13 |
10.02 |
9.22 |
10.04 |
10.05 |
9.95 |
经计算得
,
,其中
为抽取的第
 个零件的尺寸,
.
个零件的尺寸,
.
用样本平均数 作为 的估计值 ,用样本标准差 作为 的估计值 ,利用估计值判断是否需对当天的生产过程进行检查?剔除 之外的数据,用剩下的数据估计 和 (精确到0.01).
附:若随机变量 服从正态分布 ,则 ,
, .
如图,在四棱锥 中, ,且 .
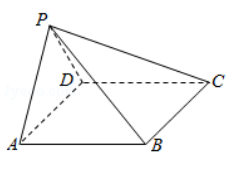
(1)证明:平面 平面 ;
(2)若 , ,求二面角 的余弦值.
△ABC的内角A,B,C的对边分别为a,b,c,已知 的面积为
(1)求 ;
(2)若 , ,求 的周长.
[选修4-5:不等式选讲]
已知函数 .
(1)当 时,求不等式 的解集;
(2)设函数 ,当 时, ,求a的取值范围.
[选修4-4:坐标系与参数方程]
在直角坐标系 中,曲线 的参数方程为 ,以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线 的极坐标方程为 .
(1)写出 的普通方程和 的直角坐标方程;
(2)设点P在 上,点Q在 上,求 的最小值及此时P的直角坐标.
[选修4-1:几何证明选讲]如图,⊙O中 的中点为P,弦PC,PD分别交AB于E,F两点.
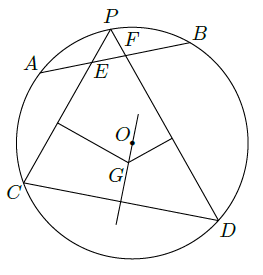
(1)若 ,求 的大小;
(2)若EC的垂直平分线与FD的垂直平分线交于点G,证明: .
设函数 .
(1)讨论 的单调性;
(2)证明当x∈(1,+∞)时,1< <x;
(3)设c>1,证明当x∈(0,1)时,1+(c﹣1)x>cx .
已知抛物线 的焦点为F,平行于x轴的两条直线 , 分别交C于A,B两点,交C的准线于P,Q两点.
(1)若F在线段AB上,R是PQ的中点,证明 ;
(2)若 的面积是 的面积的两倍,求AB中点的轨迹方程.
如图,四棱锥 中, , , , ,M为线段AD上一点, ,N为PC的中点.
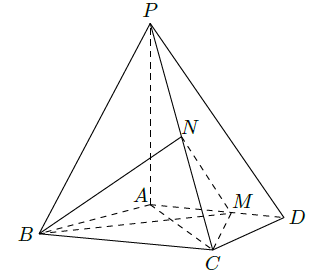
(1)证明 ;
(2)求四面体 的体积.
如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
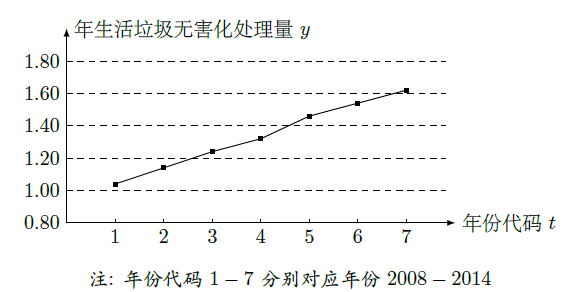
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以证明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据: , , , .
参考公式: ,回归方程 中斜率和截距的最小二乘估计公式分别为:
, .
试题篮
()