已知函数
,其中
.
(Ⅰ)讨论
的单调性;
(Ⅱ)设曲线
与
轴正半轴的交点为
,曲线在点
处的切线方程为
,求证:对于任意的正实数
,都有
;
(Ⅲ)若关于
的方程
(
为实数)有两个正实根
,求证:
已知椭圆 的左焦点为 ,离心率为 ,点M在椭圆上且位于第一象限,直线 被圆 截得的线段的长为 ,
(Ⅰ)求直线
的斜率;
(Ⅱ)求椭圆的方程;
(Ⅲ)设动点
在椭圆上,若直线
的斜率大于
,求直线
(
为原点)的斜率的取值范围.
已知数列
满足
(
),
,
,且
,
,
成等差数列.
(Ⅰ)求
的值和
的通项公式;
(Ⅱ)设
,
,求数列
的前
项和.
如图,在四棱柱 中,侧棱 , ,且点M和N分别为 的中点.

(Ⅰ)求证:
平面
;
(Ⅱ)求二面角
的正弦值;
(Ⅲ)设
为棱
上的点,若直线
和平面
所成角的正弦值为
,求线段
的长
为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(Ⅰ)设
为事件"选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会"求事件
发生的概率;
(Ⅱ)设
为选出的4人中种子选手的人数,求随机变量
的分布列和数学期望.
已知函数
,其中
.
(Ⅰ)设
为
的导函数,讨论
的单调性;
(Ⅱ)证明:存在
,使得
恒成立,且
在区间
内有唯一解.
如图,椭圆E: 的离心率是 ,点 在短轴 上,且
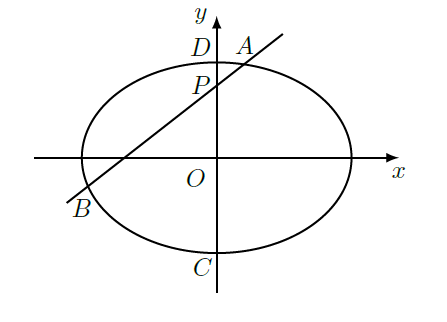
(Ⅰ)求椭圆
的方程;
(Ⅱ)设
为坐标原点,过点
的动直线与椭圆交于
两点.是否存在常数
,使得
为定值?若存在,求
的值;若不存在,请说明理由.
已知
、
、
为
的内角,
、
是关于方程
两个实根.
(Ⅰ)求
的大小
(Ⅱ)若
,
 ,求
的值
,求
的值
一个正方体的平面展开图及该正方体的直观图的示意图如图所示:
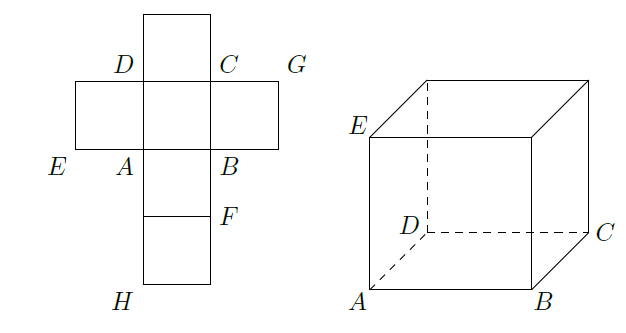
(Ⅰ)请按字母
标记在正方体相应地顶点处(不需要说明理由)
(Ⅱ)判断平面
与平面
的位置关系,并说明你的结论.
(Ⅲ)证明:直线
平面
.
一辆小客车上有5个座位,其座位号为1,2,3,4,5,乘客
的座位号分别为1,2,3,4,5,他们按照座位号顺序先后上车,乘客P1因身体原因没有坐自己号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位.如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
(Ⅰ)若乘客
坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
| 乘客 |
|
|
|
|
|
| 座位号 |
3 |
2 |
1 |
4 |
5 |
| 3 |
2 |
4 |
5 |
1 |
|
(Ⅱ)若乘客 坐到了2号座位,其他乘客按规则就坐,求乘客 坐到5号座位的概率.
设数列
的前
项和
满足
,且
成等差数列.
(Ⅰ)求数列的通项公式;
(Ⅱ)设数列
的前
项和为
,求
.
已知函数
,其中
.
(1)设
是
的导函数,评论
的单调性;
(2)证明:存在
,使得
在区间
内恒成立,且
在
内有唯一解.
如图,椭圆
的离心率是
,过点
的动直线
与椭圆相交于
两点,当直线
平行与
轴时,直线
被椭圆
截得的线段长为
.
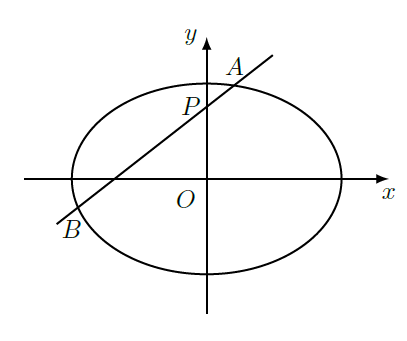
(1)求椭圆
的方程;
(2)在平面直角坐标系
中,是否存在与点
不同的定点
,使得
恒成立?若存在,求出点
的坐标;若不存在,请说明理由.
试题篮
()