(本小题满分12分)为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到如下的列联表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
20 |
5 |
25 |
| 女生 |
10 |
15 |
25 |
| 合计 |
30 |
20 |
50 |
(1)用分层抽样的方法在喜欢打蓝球的学生中抽6人,其中男生抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女生的概率.
(3)为了研究喜欢打蓝球是否与性别有关,计算出 ,你有多大的把握认为是否喜欢打蓝球与性别有关?
,你有多大的把握认为是否喜欢打蓝球与性别有关?
附:(临界值表供参考)
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
如图,过点 作抛物线
作抛物线 的切线
的切线 ,切点
,切点 在第二象限.
在第二象限.
(1)求切点 的纵坐标;
的纵坐标;
(2)若离心率为 的椭圆
的椭圆 恰好经过切点
恰好经过切点 ,设切线
,设切线 交椭圆的另一点为
交椭圆的另一点为 ,记切线
,记切线 ,
, ,
, 的斜率分别为
的斜率分别为 ,
, ,
, ,若
,若 ,求椭圆方程.
,求椭圆方程.
某网站用“10分制”调查一社区人们的幸福度.现从调查人群中随机抽取16名,以下茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):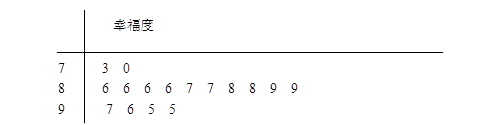
若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.
(1)从这16人中随机选取3人,记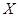 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求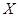 的分布列及数学期望,并求出至多有1人是“极幸福”的概率;
的分布列及数学期望,并求出至多有1人是“极幸福”的概率;
(2)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求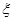 的数学期望.
的数学期望.
(本小题满分13分)已知 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为坐标原点,点
为坐标原点,点 在椭圆上,线段
在椭圆上,线段 与
与 轴的交点
轴的交点 满足
满足
(1)求椭圆的标准方程;
(2)⊙ 是以
是以 为直径的圆,一直线
为直径的圆,一直线 与⊙
与⊙ 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点 .当
.当 ,且满足
,且满足 时,求
时,求 面积
面积 的取值范围.
的取值范围.
选修4—4:坐标系与参数方程
已知椭圆C: ,直线
,直线 :
: ,
,
(Ⅰ)以原点O为极点,x轴正半轴为极轴建立极坐标系,求椭圆C与直线 的极坐标方程;
的极坐标方程;
(Ⅱ)已知P是 上一动点,射线OP交椭圆C于点R,又点Q在OP上且满足
上一动点,射线OP交椭圆C于点R,又点Q在OP上且满足 .当点P在
.当点P在 上移动时,求点Q在直角坐标系下的轨迹方程.
上移动时,求点Q在直角坐标系下的轨迹方程.
已知定点 及椭圆
及椭圆 ,过点
,过点 的动直线与该椭圆相交于
的动直线与该椭圆相交于 两点.
两点.
(Ⅰ)若线段 中点的横坐标是
中点的横坐标是 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)在 轴上是否存在点
轴上是否存在点 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知曲线 :
: ,曲线
,曲线 :
: .曲线
.曲线 的左顶点恰为曲线
的左顶点恰为曲线 的左焦点.
的左焦点.
(Ⅰ)求 的值;
的值;
(Ⅱ)设 为曲线
为曲线 上一点,过点
上一点,过点 作直线交曲线
作直线交曲线 于
于 两点. 直线
两点. 直线 交曲线
交曲线 于
于 两点. 若
两点. 若 为
为 中点,
中点,
① 求证:直线 的方程为
的方程为  ;
;
② 求四边形 的面积.
的面积.
(本小题满分12分)已知椭圆C: (a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为
(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为 b.
b.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)设b=2,直线y=kx+4与椭圆C交于不同的两点M,N,求证:直线BM与直线AN的交点G在定直线上.
(本小题满分12分)已知 ,设函数
,设函数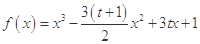 .
.
(Ⅰ)若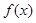 在
在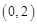 上无极值,求
上无极值,求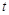 的值;
的值;
(Ⅱ)若存在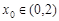 ,使得
,使得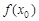 是
是 在[0, 2]上的最大值,求t的取值范围;
在[0, 2]上的最大值,求t的取值范围;
(Ⅲ)若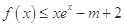 (
( 为自然对数的底数)对任意
为自然对数的底数)对任意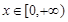 恒成立时m的最大值为1,求t的取值范围.
恒成立时m的最大值为1,求t的取值范围.
(本小题满分12分)如图,抛物线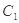 :
: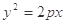 与椭圆
与椭圆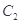 :
: 在第一象限的交点为
在第一象限的交点为 ,
, 为坐标原点,
为坐标原点, 为椭圆的右顶点,
为椭圆的右顶点, 的面积为
的面积为 .
.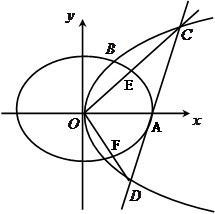
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)过 点作直线
点作直线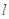 交
交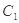 于
于 、
、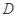 两点,射线
两点,射线 、
、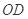 分别交
分别交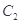 于
于 、
、 两点,记
两点,记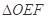 和
和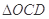 的面积分别为
的面积分别为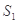 和
和 ,问是否存在直线
,问是否存在直线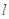 ,使得
,使得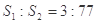 ?若存在,求出直线
?若存在,求出直线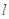 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分15分)已知数列 的首项
的首项 ,
, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前n项和
的前n项和 ;
;
(3)求证: ,
, .
.
在平面直角坐标系上,设不等式组 所表示的平面区域为
所表示的平面区域为 ,记
,记 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为 .则
.则 = ,经猜想可得到
= ,经猜想可得到 = .
= .
试题篮
()