(本题满分16分,第1小题4分,第2小题7分,第3小题5分)
如图,射线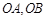 所在的直线的方向向量分别为
所在的直线的方向向量分别为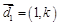 ,
, ,点
,点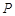 在
在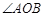 内,
内, 于
于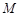 ,
,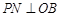 于
于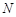 ;
;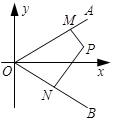
(1)若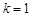 ,
,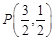 ,求
,求 的值;
的值;
(2)若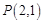 ,
,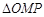 的面积为
的面积为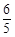 ,求
,求 的值;
的值;
(3)已知 为常数,
为常数,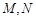 的中点为
的中点为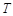 ,且
,且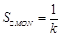 ,当
,当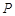 变化时,求动点
变化时,求动点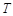 轨迹方程;
轨迹方程;
已知函数 (
( 为实数).
为实数).
(Ⅰ)当 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;
(Ⅱ)设函数 (其中
(其中 为常数),若函数
为常数),若函数 在区间
在区间 上不存在极值,且存在
上不存在极值,且存在 满足
满足
 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)已知 ,求证:
,求证: .
.
设是等差数列,是各项都为正整数的等比数列,且,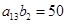 ,
,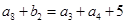 ,
,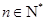 .
.
(Ⅰ)求,的通项公式;
(Ⅱ)若数列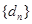 满足
满足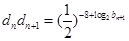 (
(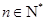 ),且
),且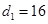 ,试求
,试求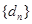 的通项公式及其前
的通项公式及其前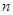 项和
项和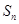 .
.
已知双曲线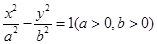 的右焦点为
的右焦点为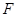 ,过
,过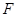 作斜率为
作斜率为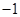 的直线交双曲线的渐近线于点
的直线交双曲线的渐近线于点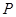 ,点
,点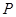 在第一象限,
在第一象限,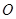 为坐标原点,若
为坐标原点,若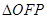 的面积为
的面积为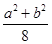 ,则该双曲线的离心率为
,则该双曲线的离心率为
A.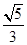 |
B.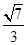 |
C.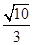 |
D.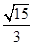 |
(本小题满分14分)
如图,摩天轮的半径OA为50m,它的最低点A距地面的高度忽略不计.地面上有一长度为240m的景观带MN,它与摩天轮在同一竖直平面内,且AM=60m.点P从最低点A处按逆时针方向转动到最高点B处,记ÐAOP=q,q∈(0,π).

(1)当q=时,求点P距地面的高度PQ;
(2)试确定q的值,使得ÐMPN取得最大值.
如图所示,在确定的四面体 中,截面
中,截面 平行于对棱
平行于对棱 和
和 .
.
(1)若 ⊥
⊥ ,则截面
,则截面 与侧面
与侧面 垂直;
垂直;
(2)当截面四边形 面积取得最大值时,
面积取得最大值时, 为
为 中点;
中点;
(3)截面四边形 的周长有最小值;
的周长有最小值;
(4)若 ⊥
⊥ ,
, ,则在四面体内存在一点
,则在四面体内存在一点 到四面体
到四面体 六条棱的中点的距离相等.上述说法正确的是 .
六条棱的中点的距离相等.上述说法正确的是 .
(本题满分14分)
已知数列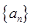 满足
满足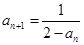 (
( ),
), ,记数列
,记数列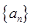 的前
的前 项和为
项和为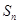 ,
,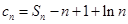 .
.
(I)令 ,求证数列
,求证数列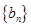 为等差数列,并求其通项公式;
为等差数列,并求其通项公式;
(II)证明: (i)对任意正整数 ,
, 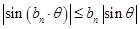 ;
;
(ii)数列 从第2项开始是递增数列.
从第2项开始是递增数列.
数列
足:
.
(1)求
的值;
(2)求数列
的前
项和
;
(3)令
,证明:数列
的前
项和
满足
.
如图,三角形
所在的平面与长方形
所在的平面垂直,
,
,
,点
是
的中点,点
、
分别在线段
、
上,且
,
.

(1)证明:
;
(2)求二面角
的正切值;
(3)求直线
与直线
所成角的余弦值.
如图,在平面直角坐标系
中,已知椭圆
的离心率为
,且右焦点
到左准线l的距离为3.
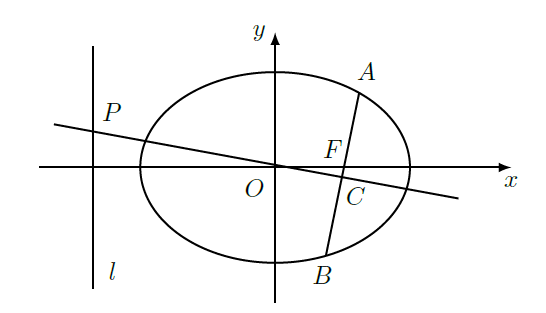
(1)求椭圆的标准方程;
(2)过
的直线与椭圆交于
两点,线段
的垂直平分线分别交直线
和
于点
,若
,求直线
的方程.
如图,椭圆
(
)的左右焦点分别为
,
,且过
的直线交椭圆于
两点,且
.

(Ⅰ)若
,
|,求椭圆的标准方程.
(Ⅱ)若
,且
,试确定椭圆离心率的取值范围.
如图,三棱锥 中, 平面 分别为线段 上的点,且

(1)证明: 平面
(2)求二面角 的余弦值。
试题篮
()