已知椭圆
上两个不同的点
关于直线
对称.
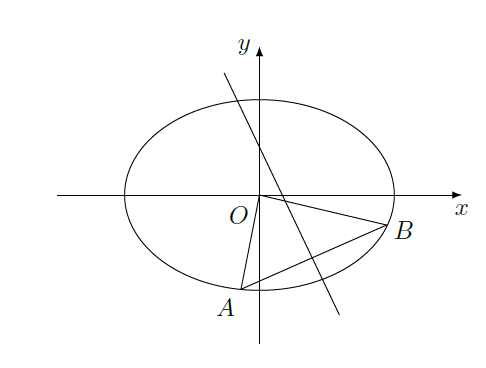
(1)求实数
的取值范围;
(2)求
面积的最大值(
为坐标原点).
已知函数
,记
是
在区间
上的最大值.
(1)证明:当
时,
;
(2)当
,
满足
,求
的最大值.
在直角坐标系中,直线
,圆
,以坐标原点为极点,
轴正半轴为极轴建立极坐标系.
(Ⅰ)求的极坐标方程.
(Ⅱ)若直线的极坐标方程为
,设
的交点为
,求
的面积.
已知过点
且斜率为
的直线
与圆
交于
两点.
(Ⅰ)求
的取值范围;
(Ⅱ)
,其中
为坐标原点,求
.
已知函数
.
(Ⅰ)当
为何值时,
轴为曲线
的切线;
(Ⅱ)用
表示
中的最小值,设函数
,讨论
)零点的个数.
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费
(单位:千元)对年销售量
(单位:
)和年利润
(单位:千元)的影响,对近8年的年宣传费
和年销售量
(
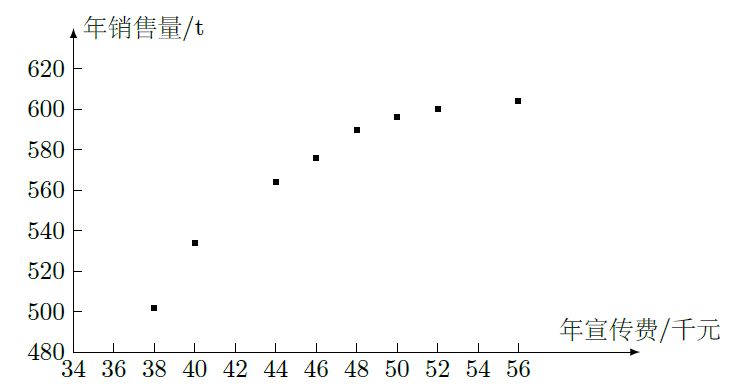
=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
 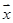 |
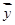 |
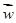 |
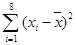 |
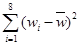 |
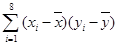 |
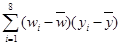 |
| 46.6 |
56.3 |
6.8 |
289.8 |
1.6 |
1469 |
108.8 |
表中 ,
,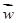 =
=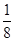
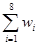
(Ⅰ)根据散点图判断,y=a+bx与y=c+d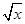 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利率z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费x为何值时,年利率的预报值最大?
附:对于一组数据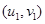 ,
,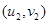 ,……,
,……,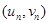 ,其回归线
,其回归线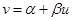 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
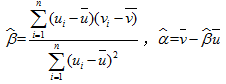
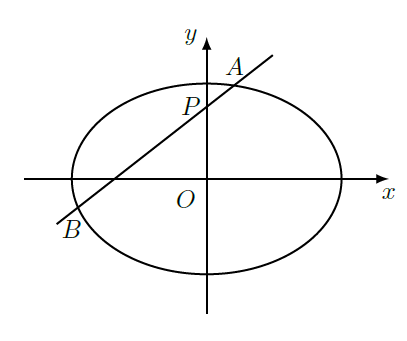
如图,椭圆
的离心率是
,过点
的动直线
与椭圆相交于
两点,当直线
平行与
轴时,直线
被椭圆
截得的线段长为
.
(1)求椭圆
的方程;
(2)在平面直角坐标系
中,是否存在与点
不同的定点
,使得
恒成立?若存在,求出点
的坐标;若不存在,请说明理由.
已知数列
与
满足
.
(1)若
,且
,求数列
的通项公式;
(2)设
的第
项是最大项,即
,求证:数列
的第
项是最大项;
(3)设
,求
的取值范围,使得
有最大值
与最小值
,且
.
已知椭圆
,过原点的两条直线
和
分别于椭圆交于
和
,记得到的平行四边形
的面积为
.
(1)设
,用
的坐标表示点
到直线
的距离,并证明
;
(2)设
与
的斜率之积为
,求面积
的值.
如图1,在直角梯形 中, , 是 的中点, 是 与 的交点,将 沿 折起到图2中 的位置,得到四棱锥 .

(Ⅰ)证明:
平面
;
(Ⅱ)当平面
平面
时,四棱锥
的体积为
,求
的值.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 在如图所示的阳马
中,侧棱
底面
,且
,点
是
的中点,连接
.

(Ⅰ)证明:
平面
. 试判断四面体
是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(Ⅱ)记阳马
的体积为
,四面体
的体积为
,求
的值.
已知数列的各项均为正数,
,
为自然对数的底数.
(Ⅰ)求函数的单调区间,并比较
与
的大小;
(Ⅱ)计算,由此推测计算
的公式,并给出证明;
(Ⅲ)令,数列
,
的前
项和分别记为
, 证明:
.
一种作图工具如图1所示.是滑槽
的中点,短杆
可绕
转动,长杆
通过
处铰链与
连接,
上的栓子
可沿滑槽
滑动,且
,
.当栓子
在滑槽
内作往复运动时,带动
绕
转动一周(
不动时,
也不动),
处的笔尖画出的曲线记为
.以
为原点,
所在的直线为
轴建立如图2所示的平面直角坐标系.

(Ⅰ)求曲线的方程;
(Ⅱ)设动直线与两定直线
和
分别交于
两点.若直线
总与曲线
有且只有一个公共点,试探究:
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
某厂用鲜牛奶在某台设备上生产
两种奶制品.生产1吨
产品需鲜牛奶2吨,使用设备1小时,获利1000元;生产1吨
产品需鲜牛奶1.5吨,使用设备1.5小时,获利1200元.要求每天
产品的产量不超过
产品产量的2倍,设备每天生产
两种产品时间之和不超过12小时.假定每天可获取的鲜牛奶数量
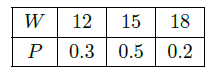
(单位:吨)是一个随机变量,其分布列为
该厂每天根据获取的鲜牛奶数量安排生产,使其获利最大,因此每天的最大获利 (单位:元)是一个随机变量.
(Ⅰ)求
的分布列和均值;
(Ⅱ)若每天可获取的鲜牛奶数量相互独立,求3天中至少有1天的最大获利超过10000元的概率.
设椭圆的方程为
,点
为坐标原点,点
的坐标为
,点
的坐标为
,点
在线段
上,满足
,直线
的斜率为
.
(Ⅰ)求的离心率
;
(Ⅱ)设点的坐标为
,
为线段
的中点,点N关于直线
的对称点的纵坐标为
,求
的方程.
试题篮
()