过抛物线: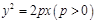 的焦点F作倾斜角为
的焦点F作倾斜角为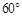 的直线
的直线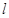 ,若直线
,若直线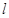 与抛物线在第一象限的交点为A,并且点A也在双曲线:
与抛物线在第一象限的交点为A,并且点A也在双曲线: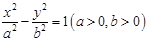 的一条渐近线上,则双曲线的离心率为( )
的一条渐近线上,则双曲线的离心率为( )
A.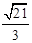 |
B.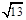 |
C.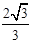 |
D.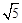 |
(本小题满分12分)设函数 .
.
(1)若函数 在
在 处有极值,求函数
处有极值,求函数 的最大值;
的最大值;
(2)①是否存在实数 ,使得关于
,使得关于 的不等式
的不等式 在
在 上恒成立?若存在,
上恒成立?若存在,
求出 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式 .
.
(本小题满分16分)已知数列 的奇数项是首项为
的奇数项是首项为 的等差数列,偶数项是首项为
的等差数列,偶数项是首项为 的等比数列,数列
的等比数列,数列 前
前 项和为
项和为 ,且满足
,且满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求正整数
,求正整数 的值;
的值;
(3)是否存在正整数 ,使得
,使得 恰好为数列
恰好为数列 中的一项?若存在,求出所有满足条件的
中的一项?若存在,求出所有满足条件的 值,若不存在,说明理由.
值,若不存在,说明理由.
(本小题满分16分)设数列 的前
的前 项和为
项和为 ,满足
,满足
 .
.
(1)当 时,
时,
①设 ,若
,若 ,
, .求实数
.求实数 的值,并判定数列
的值,并判定数列 是否为等比数列;
是否为等比数列;
②若数列 是等差数列,求
是等差数列,求 的值;
的值;
(2)当 时,若数列
时,若数列 是等差数列,
是等差数列, ,且
,且 ,
, ,
,
求实数 的取值范围.
的取值范围.
(本小题满分14分)如图,某城市有一条公路从正西方 通过市中心
通过市中心 后转向东偏北
后转向东偏北 角方向的
角方向的 .位于该市的某大学
.位于该市的某大学 与市中心
与市中心 的距离
的距离 ,且
,且 .现要修筑一条铁路L,L在OA上设一站
.现要修筑一条铁路L,L在OA上设一站 ,在OB上设一站B,铁路在
,在OB上设一站B,铁路在 部分为直线段,且经过大学
部分为直线段,且经过大学 .其中
.其中 ,
, ,
, .
.
(1)求大学 与站
与站 的距离
的距离 ;
;
(2)求铁路 段的长
段的长 .
.
(本小题满分12分)定义在 上的函数
上的函数 满足
满足 ,
, .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 的单调区间;
的单调区间;
(3)如果 ,
, ,
, 满足
满足 ,那么称
,那么称 比
比 更靠近
更靠近 .当
.当 且
且 时,试比较
时,试比较 和
和 哪个更靠近
哪个更靠近 ,并说明理由.
,并说明理由.
(本小题满分12分)已知椭圆 :
: 的上顶点为
的上顶点为 ,且离心率为
,且离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)证明:过椭圆 :
: 上一点
上一点 的切线方程为
的切线方程为 ;
;
(3)从圆 上一点
上一点 向椭圆
向椭圆 引两条切线,切点分别为
引两条切线,切点分别为 ,
, ,当直线
,当直线 分别与
分别与 轴,
轴, 轴交于
轴交于 ,
, 两点时,求
两点时,求 的最小值.
的最小值.
对定义在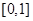 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数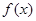 称为
称为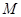 函数:
函数:
(i)对任意的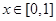 ,恒有
,恒有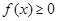 ;
;
(ii)当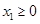 ,
,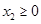 ,
,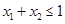 时,总有
时,总有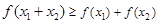 成立.
成立.
则下列四个函数中不是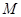 函数的个数是( )
函数的个数是( )
① ②
②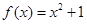 ③
③ 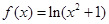 ④
④ 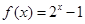
| A.1 | B.2 | C.3 | D.4 |
(本小题满分12分)最新高考改革方案已在上海和江苏开始实施,某教育机构为了解我省广大师生对新高考改革方案的看法,对某市部分学校500名师生进行调查,统计结果如下:
在全体师生中随机抽取1名“赞成改革”的人是学生的概率为0.3,且x=2y.
(Ⅰ)现从全部500名师生中用分层抽样的方法抽取50名进行问卷调查,则应抽取“不
赞成改革”的教师和学生人数各是多少?
(Ⅱ)在(Ⅰ)中所抽取的“不赞成改革”的人中,随机选出三人进行座谈,求至少有一名
教师被选出的概率。
如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中,下面四个命题中不正确的是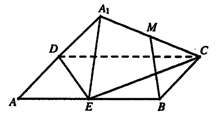
| A.|BM|是定值 |
| B.点M在某个球面上运动 |
| C.存在某个位置,使DE⊥A1 C |
| D.存在某个位置,使MB//平面A1DE |
(本小题满分13分)已知二次函数 的图象的顶点坐标为
的图象的顶点坐标为 ,且过坐标原点
,且过坐标原点 .数列
.数列 的前
的前 项和为
项和为 ,点
,点 在二次函数
在二次函数 的图象上.
的图象上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)在数列 中是否存在这样一些项:
中是否存在这样一些项:

 ,这些项都能够构成以
,这些项都能够构成以 为首项,
为首项, 为公比的等比数列
为公比的等比数列 ?若存在,写出
?若存在,写出 关于
关于 的表达式;若不存在,说明理由.
的表达式;若不存在,说明理由.
(本小题满分14分)如图,在四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形,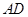 //
//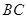 ,
,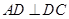 ,平面
,平面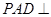 底面
底面 ,
,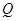 为
为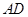 的中点,
的中点, 是棱
是棱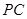 的中点,
的中点,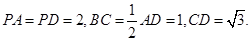
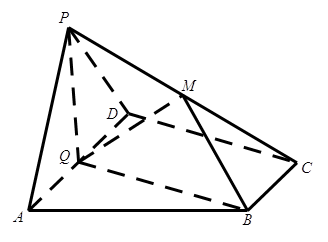
(Ⅰ)求证: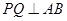 ;
;
(Ⅱ)求直线 与平面
与平面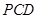 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(本小题满分14分)如图,已知椭圆 的离心率为
的离心率为  ,F1、F2为其左、右焦点,过F1的直线
,F1、F2为其左、右焦点,过F1的直线 交椭圆于A、B两点,△F1AF2的周长为
交椭圆于A、B两点,△F1AF2的周长为 .
.
(1)求椭圆的标准方程;
(2)求△AOB面积的最大值(O为坐标原点);
(本小题满分13分)在平面直角坐标系中,已知点 ,点B在直线
,点B在直线 :
: 上运动,过点B与
上运动,过点B与 垂直的直线和线段AB的垂直平分线相交于点M.
垂直的直线和线段AB的垂直平分线相交于点M.
(1)求动点M的轨迹E的方程;
(2)过(1)中轨迹E上的点 作轨迹E的切线,求切线方程.
作轨迹E的切线,求切线方程.
试题篮
()