(本小题满分12分)设数列 的首项为1,前n项和为Sn,且
的首项为1,前n项和为Sn,且 (
( ).
).
(1)求数列 的通项公式;
的通项公式;
(2)设 ,
, 是数列
是数列 的前n项和,求
的前n项和,求 .
.
(本小题满分13分)已知动点P到定点 的距离和它到定直线
的距离和它到定直线 的距离的比值为
的距离的比值为 .
.
(Ⅰ)求动点P的轨迹W的方程;
(Ⅱ)若过点F的直线与点P的轨迹W相交于M,N两点(M,N均在y轴右侧),点 、
、 ,设A,B,M,N四点构成的四边形的面积为S,求S的取值范围.
,设A,B,M,N四点构成的四边形的面积为S,求S的取值范围.
已知椭圆C: 的离心率为
的离心率为 ,且C上任意一点到两个焦点的距离之和都为4.
,且C上任意一点到两个焦点的距离之和都为4.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线 与椭圆交于P、Q,O为坐标原点,若
与椭圆交于P、Q,O为坐标原点,若 ,求证
,求证 为定值.
为定值.
已知函数 ,
,
(1)求证: ;
;
(2)设 ,求证:存在唯一的
,求证:存在唯一的 使得g(x)图象在点A(
使得g(x)图象在点A( )处的切线
)处的切线 与y=f(x)图象也相切;
与y=f(x)图象也相切;
(3)求证:对任意给定的正数a,总存在正数x,使得 成立.
成立.
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且AM ,点P是平面ABCD上的动点,且动点P到直线A1D1的距离与点P到点M的距离的平方差为1,则动点P的轨迹是( )
,点P是平面ABCD上的动点,且动点P到直线A1D1的距离与点P到点M的距离的平方差为1,则动点P的轨迹是( ) 
| A.圆 | B.抛物线 | C.双曲线 | D.椭圆 |
(本小题满分13分)设数列 满足:
满足:
① ;
;
②所有项 ;
;
③ .
.
设集合 ,将集合
,将集合 中的元素的最大值记为
中的元素的最大值记为 ,即
,即 是数列
是数列 中满足不等式
中满足不等式 的所有项的项数的最大值.我们称数列
的所有项的项数的最大值.我们称数列 为数
为数 的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
(Ⅰ)若数列 的伴随数列为1,1,1,2,2,2,3,请写出数列
的伴随数列为1,1,1,2,2,2,3,请写出数列 ;
;
(Ⅱ)设 ,求数列
,求数列 的伴随数列
的伴随数列 的前30项之和;
的前30项之和;
(Ⅲ)若数列 的前
的前 项和
项和 (其中
(其中 常数),求数列
常数),求数列 的伴随数列
的伴随数列
的前 项和
项和 .
.
(本小题满分14分)已知函数
(Ⅰ)若函数 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数 的最小值;
的最小值;
(Ⅱ)方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围;
的取值范围;
(Ⅲ)在函数 的图象上是否存在不同两点
的图象上是否存在不同两点 ,线段
,线段 的中点的横坐标为
的中点的横坐标为 ,有
,有 成立?若存在,请求出
成立?若存在,请求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(1)(本小题6分)在平面直角坐标系中,已知某点 ,直线
,直线 .求证:点P到直线
.求证:点P到直线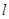 的距离
的距离
(2)(本小题7分)已知抛物线C:  的焦点为F,点P(2,0),O为坐标原点,过P的直线
的焦点为F,点P(2,0),O为坐标原点,过P的直线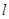 与抛物线C相交于A,B两点,若向量
与抛物线C相交于A,B两点,若向量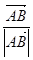 在向量
在向量 上的投影为n,且
上的投影为n,且 ,求直线
,求直线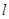 的方程.
的方程.
(本小题满分12分)如图,圆 与
与 轴相切于点
轴相切于点 ,与
,与 轴正半轴相交于两点
轴正半轴相交于两点 (点
(点 在点
在点 的左侧),且
的左侧),且 .
.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)过点 任作一条直线与椭圆
任作一条直线与椭圆 相交于两点
相交于两点 ,连接
,连接 ,求证:
,求证: .
.
(本小题满分12分)已知正项数列 的首项
的首项 ,前
,前 项和
项和 满足
满足 .
.
(1)求证: 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(2)记数列 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
试题篮
()