(本小题满分12分)
已知函数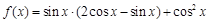 .
.
(Ⅰ)讨论函数 在
在 上的单调性;
上的单调性;
(Ⅱ)设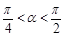 ,且
,且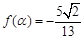 ,求
,求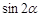 的值.
的值.
(本小题满分18分)已知数列 ,
, .
.
(1)求证:数列 为等比数列;
为等比数列;
(2)数列 中,是否存在连续的三项,这三项构成等比数列?试说明理由;
中,是否存在连续的三项,这三项构成等比数列?试说明理由;
(3)设 ,其中
,其中 为常数,且
为常数,且 ,
, ,求
,求 .
.
(本小题满分14分)已知函数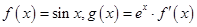 ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(1)求曲线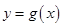 在点
在点 处的切线方程;
处的切线方程;
(2)若对任意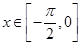 ,不等式
,不等式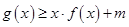 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)试探究当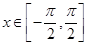 时,方程
时,方程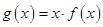 的解的个数,并说明理由.
的解的个数,并说明理由.
(本小题满分14分)在平面直角坐标系 中,已知动点
中,已知动点 到两个定点
到两个定点 ,
, 的距离的和为定值
的距离的和为定值 .
.
(1)求点 运动所成轨迹
运动所成轨迹 的方程;
的方程;
(2)设 为坐标原点,若点
为坐标原点,若点 在轨迹
在轨迹 上,点
上,点 在直线
在直线 上,且
上,且 ,试判断直线
,试判断直线 与圆
与圆 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
在平面直角坐标系 中,动点
中,动点 到两点
到两点 ,
, 的距离之和等于
的距离之和等于 ,设点
,设点 的轨迹为曲线
的轨迹为曲线 ,直线
,直线 与曲线
与曲线 交于点
交于点 (点
(点 在第一象限).
在第一象限).
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)已知 为曲线
为曲线 的左顶点,平行于
的左顶点,平行于 的直线
的直线 与曲线
与曲线 相交于
相交于 两点.判断直线
两点.判断直线 是否关于直线
是否关于直线 对称,并说明理由.
对称,并说明理由.
(本小题12分)已知如图,圆 和抛物线
和抛物线 ,圆的切线
,圆的切线 与抛物线
与抛物线 交于不同的点
交于不同的点 ,
, .
.
(1)当直线 的斜率为
的斜率为 时,求线段
时,求线段 的长;
的长;
(2)设点 和点
和点 关于直线
关于直线 对称,问是否存在圆的切线
对称,问是否存在圆的切线 使得
使得 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
香港违法“占中”行动对香港的经济、政治、社会及民生造成重大损失,据香港科技大学经济系教授雷鼎鸣测算,仅香港的“占中”行动开始后一个多月的时间,保守估计造成经济损失 亿港元,相等于平均每名港人承受了
亿港元,相等于平均每名港人承受了 万港元的损失,为了挽回经济损失,某厂家拟在新年举行大型的促销活动,经测算某产品当促销费用为
万港元的损失,为了挽回经济损失,某厂家拟在新年举行大型的促销活动,经测算某产品当促销费用为 万元时,销售量
万元时,销售量 万件满足
万件满足 (其中
(其中 ,
, 为正常数).现假定生产量与销售量相等,已知生产该产品
为正常数).现假定生产量与销售量相等,已知生产该产品 万件还需投入成本
万件还需投入成本 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为 万元/万件.
万元/万件.
(1)将该产品的利润 万元表示为促销费用
万元表示为促销费用 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
(本小题满分13分)如图,已知圆E: ,点
,点 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
(Ⅰ)求动点Q的轨迹 的方程;
的方程;
(Ⅱ)设直线 与(Ⅰ)中轨迹
与(Ⅰ)中轨迹 相交于
相交于 两点,直线
两点,直线 的斜率分别为
的斜率分别为 (其中
(其中 ).△
).△ 的面积为
的面积为 , 以
, 以 为直径的圆的面积分别为
为直径的圆的面积分别为 .若
.若 恰好构成等比数列, 求
恰好构成等比数列, 求 的取值范围.
的取值范围.
已知矩形 的周长为
的周长为 ,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为 .
,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为 .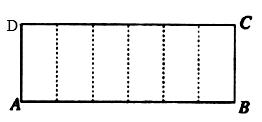
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
(文)对于曲线 ,若存在非负实数
,若存在非负实数 和
和 ,使得曲线
,使得曲线 上任意一点
上任意一点 ,
, 恒成立(其中
恒成立(其中 为坐标原点),则称曲线
为坐标原点),则称曲线 为有界曲线,且称
为有界曲线,且称 的最小值
的最小值 为曲线
为曲线 的外确界,
的外确界, 的最大值
的最大值 为曲线
为曲线 的内确界.
的内确界.
(1)写出曲线 的外确界
的外确界 与内确界
与内确界 ;
;
(2)曲线 与曲线
与曲线 是否为有界曲线?若是,求出其外确界与内确界;若不是,请说明理由;
是否为有界曲线?若是,求出其外确界与内确界;若不是,请说明理由;
(3)已知曲线 上任意一点
上任意一点 到定点
到定点 的距离之积为常数
的距离之积为常数 ,求曲线
,求曲线 的外确界与内确界.
的外确界与内确界.
本题共有2个小题,第1小题满分6分,第2小题满分8分
沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时。如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的 (细管长度忽略不计).
(细管长度忽略不计).
(1)如果该沙漏每秒钟漏下0.02cm3的沙,则该沙漏的一个沙时为多少秒(精确到1秒)?
(2)细沙全部漏入下部后,恰好堆成个一盖住沙漏底部的圆锥形沙堆,求此锥形沙堆的高度(精确到0.1cm).
试题篮
()