(本小题满分12分)如图所示,抛物线C1:x2=4y在点A,B处的切线垂直相交于点P,直线AB与椭圆,C2: 相交于C,D两点.
相交于C,D两点.
(Ⅰ)求抛物线C1的焦点F与椭圆C2的左焦点F1的距离;
(Ⅱ)设点P到直线AB的距离为d,是否存在直线AB,使得|AB|,d,|CD|成等比数列?若存在,求出直线AB的方程;若不存在,请说明理由.
(本小题满分14分)已知 ,设函数
,设函数 .
.
(Ⅰ)若 在(0, 2)上无极值,求t的值;
在(0, 2)上无极值,求t的值;
(Ⅱ)若存在 ,使得
,使得 是
是 在[0, 2]上的最大值,求t的取值范围;
在[0, 2]上的最大值,求t的取值范围;
(Ⅲ)若 为自然对数的底数)对任意
为自然对数的底数)对任意 恒成立时m的最大值为1,求t的取值范围.
恒成立时m的最大值为1,求t的取值范围.
(本小题满分12分)已知等比数列{an}的公比 ,前n项和为Sn,S3=7,且
,前n项和为Sn,S3=7,且 ,
, ,
,
成等差数列,数列{bn}的前n项和为Tn, ,其中
,其中 N*.
N*.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{bn}的通项公式;
(Ⅲ)设 ,
, ,
, ,求集合C中所有元素之和.
,求集合C中所有元素之和.
(本小题满分14分)给定正奇数 ,数列
,数列 :
: 是1,2,…,
是1,2,…, 的一个排列,定义E(
的一个排列,定义E( ,…,
,…, )
) 为数列
为数列 :
: ,
, ,…,
,…, 的位差和.
的位差和.
(1)当 时,求数列
时,求数列 :1,3,4,2,5的位差和;
:1,3,4,2,5的位差和;
(2)若位差和E( ,
, ,…,
,…, )=4,求满足条件的数列
)=4,求满足条件的数列 :
: ,
, ,…,
,…, 的个数;
的个数;
(3)若位差和 ,求满足条件的数列
,求满足条件的数列 :
: 的个数.
的个数.
已知 ,函数
,函数 的零点从小到大依次为
的零点从小到大依次为 ,
, .
.
(Ⅰ)若 (
( ),试写出所有的
),试写出所有的 值;
值;
(Ⅱ)若 ,
, ,
, ,求证:
,求证:  ;
;
(Ⅲ)若 ,
, ,
, ,试把数列
,试把数列 的前
的前 项及
项及 按从小到大的顺序排列。(只要求写出结果).
按从小到大的顺序排列。(只要求写出结果).
在如图所示的几何体中, 四边形 是正方形,
是正方形, ,
, ,且
,且 ,
, ,
, .
.
(Ⅰ)若 与
与 交于点
交于点 ,求证:
,求证:  平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(本小题满分13分)
若有穷数列 ,
, ,
, (
( 是正整数)满足条件:
是正整数)满足条件: ,则称其为“对称数列”.例如,
,则称其为“对称数列”.例如, 和
和 都是“对称数列”.
都是“对称数列”.
(Ⅰ)若 是25项的“对称数列”,且
是25项的“对称数列”,且

 ,
, 是首项为1,公比为2的等比数列.求
是首项为1,公比为2的等比数列.求 的所有项和
的所有项和 ;
;
(Ⅱ)若 是50项的“对称数列”,且
是50项的“对称数列”,且

 ,
, 是首项为1,公差为2的等差数列.求
是首项为1,公差为2的等差数列.求 的前
的前 项和
项和 ,
, .
.
已知等差数列 的前n项和为
的前n项和为 ,且
,且 .数列
.数列 的前n项和为
的前n项和为 ,且
,且 ,
, .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)设 , 求数列
, 求数列 的前
的前 项和
项和 .
.
已知函数 ,各项均不相等的有限项数列
,各项均不相等的有限项数列 的各项
的各项 满足
满足 .令
.令 ,
, 且
且 ,例如:
,例如: .
.
(Ⅰ)若 ,数列
,数列 的前n项和为Sn,求S19的值;
的前n项和为Sn,求S19的值;
(Ⅱ)试判断下列给出的三个命题的真假,并说明理由。
①存在数列 使得
使得 ;②如果数列
;②如果数列 是等差数列,则
是等差数列,则 ;
;
③如果数列 是等比数列,则
是等比数列,则 。
。
(本小题满分13分)已知等比数列 的公比
的公比 ,前n项和为
,前n项和为 且
且 成等差数列,数列
成等差数列,数列 的前n项和为
的前n项和为 ,其中
,其中 。
。
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的通项公式;
的通项公式;
(3)设 ,
, ,求集合
,求集合 中的所有元素之和。
中的所有元素之和。
如图,在透明塑料制成的长方体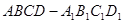 容器内灌进一些水,将容器底面一边
容器内灌进一些水,将容器底面一边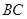 固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法: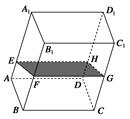
①水的部分始终呈棱柱状;
②水面四边形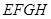 的面积不改变;
的面积不改变;
③棱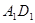 始终与水面
始终与水面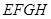 平行;
平行;
④当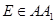 时,
时,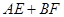 是定值.
是定值.
其中正确说法是 .
已知椭圆的焦点坐标是 ,
, ,过点
,过点 垂直于长轴的直线交椭圆与
垂直于长轴的直线交椭圆与 两点, 且
两点, 且 .
.
(1)求椭圆的方程.
(2)过 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点 , 则
, 则 的内切圆面积是否存在最大值?若存在, 则求出这个最大值及此时的直线方程; 若不存在,请说明理由.
的内切圆面积是否存在最大值?若存在, 则求出这个最大值及此时的直线方程; 若不存在,请说明理由.
试题篮
()