(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线 的参数方程为
的参数方程为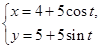 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
(1)把 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(2)求 与
与 交点的极坐标
交点的极坐标 .
.
定义:若各项为正实数的数列 满足
满足 ,则称数列
,则称数列 为“算术平方根递推数列”.
为“算术平方根递推数列”.
已知数列 满足
满足 且
且 点
点 在二次函数
在二次函数 的图像上.
的图像上.
(1)试判断数列
 是否为算术平方根递推数列?若是,请说明你的理由;
是否为算术平方根递推数列?若是,请说明你的理由;
(2)记
 ,求证:数列
,求证:数列 是等比数列,并求出通项公式
是等比数列,并求出通项公式 ;
;
(3)从数列 中依据某种顺序自左至右取出其中的项
中依据某种顺序自左至右取出其中的项 ,把这些项重新组成一个新数列
,把这些项重新组成一个新数列 :
: .若数列
.若数列 是首项为
是首项为 、公比为
、公比为 的无穷等比数列,且数列
的无穷等比数列,且数列 各项的和为
各项的和为 ,求正整数
,求正整数 的值.
的值.
已知函数 ,函数
,函数 是函数
是函数 的反函数.
的反函数.
(1)求函数 的解析式,并写出定义域
的解析式,并写出定义域 ;
;
(2)设 ,若函数
,若函数 在区间
在区间 内的图像是不间断的光滑曲线,求证:函数
内的图像是不间断的光滑曲线,求证:函数 在区间
在区间 内必有唯一的零点(假设为
内必有唯一的零点(假设为 ),且
),且 .
.
已知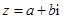
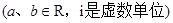 ,
, ,定义:
,定义: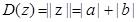 ,
,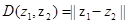 .给出下列命题:
.给出下列命题:
(1)对任意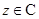 ,都有
,都有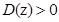 ;
;
(2)若 是复数
是复数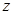 的共轭复数,则
的共轭复数,则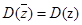 恒成立;
恒成立;
(3)若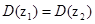
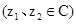 ,则
,则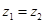 ;
;
(4)对任意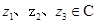 ,结论
,结论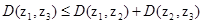 恒成立,则其中真命题是[答]( ).
恒成立,则其中真命题是[答]( ).
| A.(1)(2)(3)(4) | B.(2)(3)(4) | C.(2)(4) | D.(2)(3) |
已知函数 是定义域为
是定义域为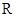 的偶函数. 当
的偶函数. 当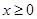 时,
时,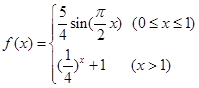 若关于
若关于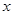 的方程
的方程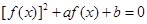 (
(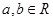 ),有且仅有6个不同实数根,则实数
),有且仅有6个不同实数根,则实数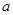 的取值范围是( )
的取值范围是( )
A.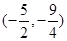 |
B.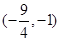 |
C.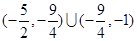 |
D.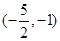 |
已知 ,
,
且 .
.
(Ⅰ)当 时,求
时,求 在
在 处的切线方程;
处的切线方程; (Ⅱ)当
(Ⅱ)当 时,设
时,设 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为 (闭区间
(闭区间 的长度定义为
的长度定义为 ),试求
),试求 的最大值;
的最大值;
(Ⅲ)是否存在这样的 ,使得当
,使得当 时,
时, ?若存在,求出
?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知椭圆 的离心率为
的离心率为 ,椭圆的左、右两个顶点分别为
,椭圆的左、右两个顶点分别为 ,
, ,直线
,直线 与椭圆相交于
与椭圆相交于 两点,经过三点
两点,经过三点 的圆与经过三点
的圆与经过三点 的圆分别记为圆C1与圆C2.
的圆分别记为圆C1与圆C2.
(1)求椭圆的方程;
(2)求证:无论 如何变化,圆C1与圆C2的圆心距是定值;
如何变化,圆C1与圆C2的圆心距是定值;
(3)当 变化时,求圆C1与圆C2的面积的和
变化时,求圆C1与圆C2的面积的和 的最小值.
的最小值.
(本小题满分14分)如图,已知圆E: ,点
,点 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
(Ⅰ)求动点Q的轨迹 的方程;
的方程;
(Ⅱ)设直线 与(Ⅰ)中轨迹
与(Ⅰ)中轨迹 相交于
相交于 两点,直线
两点,直线 的斜率分别为
的斜率分别为
 .△
.△ 的面积为
的面积为 ,以
,以 为直径的圆的面积分别为
为直径的圆的面积分别为 .若
.若 恰好构成等比数列,求
恰好构成等比数列,求 的取值范围.
的取值范围.
(本小题满分13分)如图,已知圆E: ,点
,点 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
(Ⅰ)求动点Q的轨迹 的方程;
的方程;
(Ⅱ)设直线 与(Ⅰ)中轨迹
与(Ⅰ)中轨迹 相交于
相交于 两点, 直线
两点, 直线 的斜率分别为
的斜率分别为 (其中
(其中 ).△
).△ 的面积为
的面积为 , 以
, 以 为直径的圆的面积分别为
为直径的圆的面积分别为 .若
.若 恰好构成等比数列, 求
恰好构成等比数列, 求 的取值范围.
的取值范围.
试题篮
()