如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形 与正方形 .连结 , 相交于点 、 与 相交于点 .若 ,则 的值是

A. B. C. D.
如图,四边形 ABCD是菱形,点 E、 F分别在边 AB、 AD的延长线上,且 ,连接 CE、 CF.求证: .
如图,已知 是 斜边 上的高线, .以 为圆心, 为半径的圆交 于点 ,过点 作 的切线 ,交 于点 .则下列结论中错误的是

A. B. C. D.
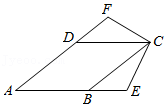
如图,四边形 为菱形, ,延长 到 ,在 内作射线 ,使得 ,过点 作 ,垂足为 ,若 ,则对角线 的长为 (结果保留根号)

如图是一张矩形纸片,点 在 边上,把 沿直线 对折,使点 落在对角线 上的点 处,连接 .若点 , , 在同一条直线上, ,则 , .

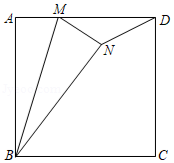
如图,在正方形 中, , 是 边上的一点, 。将 沿 对折至 ,连接 ,则 的长是
| A. |
|
B. |
|
C. |
3 |
D. |
|
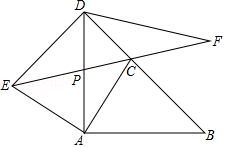
如图, 由 绕点 按逆时针方向旋转 得到,且点 的对应点 恰好落在 的延长线上, , 相交于点 .
(1)求 的度数;
(2) 是 延长线上的点,且 .
①判断 和 的数量关系,并证明;
②求证: .
如图, 中,点 为边 的中点,连接 ,将 沿直线 翻折至 所在平面内,得 ,连接 ,分别与边 交于点 ,与 交于点 .若 , ,则 的长为 .

如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

在① ,② ,③ 这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.
问题:如图,在 中, ,点 在 边上(不与点 ,点 重合),点 在 边上(不与点 ,点 重合),连接 , , 与 相交于点 .若 ① ② 或 ③ ,求证: .
注:如果选择多个条件分别作答,按第一个解答计分.

如图, 中, , ,点 ,点 ,反比例函数 的图象经过点 .
(1)求反比例函数的解析式;
(2)将直线 向上平移 个单位后经过反比例函数 图象上的点 ,求 , 的值.

试题篮
()