如图,在正方形 中,对角线 , 相交于点 ,点 , 是对角线 上的两点,且 .连接 , , , .
(1)证明: .
(2)若 , ,求四边形 的周长.

如图, 、 、 、 是四根长度均为 的火柴棒,点 、 、 共线.若 , ,则线段 的长度是

| A. |
|
B. |
|
C. |
|
D. |
|
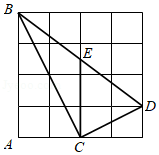
如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 为等腰直角三角形,延长 至点 使 , 是矩形,其对角线 , 交于点 ,连接 交 于点 .
(1)求证: ;
(2)求 的值.

综合与实践
问题情境:
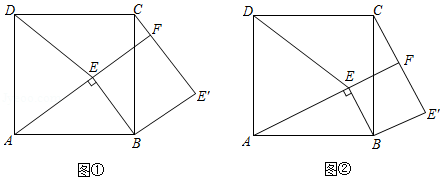
如图①,点 为正方形 内一点, ,将 绕点 按顺时针方向旋转 ,得到 (点 的对应点为点 .延长 交 于点 ,连接 .
猜想证明:
(1)试判断四边形 的形状,并说明理由;
(2)如图②,若 ,请猜想线段 与 的数量关系并加以证明;
解决问题:
(3)如图①,若 , ,请直接写出 的长.
如图, 交 于点 ,在 与 中,有下列三个条件:① ,② ,③ .请你在上述三个条件中选择两个为条件,另一个能作为这两个条件推出来的结论,并证明你的结论(只要求写出一种正确的选法).
(1)你选的条件为 、 ,结论为 ;
(2)证明你的结论.

如图, 中,点 为边 的中点,连接 ,将 沿直线 翻折至 所在平面内,得 ,连接 ,分别与边 交于点 ,与 交于点 .若 , ,则 的长为 .

如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

在① ,② ,③ 这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.
问题:如图,在 中, ,点 在 边上(不与点 ,点 重合),点 在 边上(不与点 ,点 重合),连接 , , 与 相交于点 .若 ① ② 或 ③ ,求证: .
注:如果选择多个条件分别作答,按第一个解答计分.

如图, 中, , ,点 ,点 ,反比例函数 的图象经过点 .
(1)求反比例函数的解析式;
(2)将直线 向上平移 个单位后经过反比例函数 图象上的点 ,求 , 的值.

试题篮
()