初中数学圆内接四边形的性质解答题

在一次数学实践探究活动中，小强用两条直线把平行四边形ABCD分割成四个部分，使含有一组对顶角的两个图形全等；
（ 1 ）根据小强的分割方法，你认为把平行四边形分割成满足以上全等关系的直线有    组；
（ 2 ）请在图中的三个平行四边形中画出满足小强分割方法的直线；

（ 3 ）由上述实验操作过程，你发现所画的两条直线有什么规律？
                                                                       

如图，矩形ABCD的对角线AC、BD交于点O，∠AOD=60°，AB=，AE⊥BD于点E，求OE的长。

如图，把长方形纸片ABCD沿EF折叠，使点D与点B重合，点C落在点C′的位置上．

⑴若∠1=50°，求∠2、∠3的度数；
⑵若AB=7，DE=8，求CF的长度．

如图，在梯形ABCD中，AB∥DC， DB平分∠ADC，过点A作AE∥BD，交CD的延长线于点E，且∠C＝2∠E．

⑴求证：梯形ABCD是等腰梯形．
⑵若∠BDC＝30°，AD＝5，求CD的长．

已知如下图，正方形ABCD中，E是CD边上的一点，F为BC延长线上点，CE="CF."

(1)求证：△BEC≌△DFC；
(2)若∠BEC=60°，求∠EFD的度数

如图，已知E、F分别是▱ABCD的边BC、AD上的点，且BE=DF．

（1）求证：四边形AECF是平行四边形；
（2）若BC=10，∠BAC=90°，且四边形AECF是菱形，求BE的长．

已知：如图，BC是等腰△BED底边ED上的高，四边形ABEC是平行四边形。求证：四边形ABCD是矩形．

如图，在梯形ABCD中，AD∥BC，AB＝DC＝AD，BC＝AC，求该梯形各内角的度数．
 

如图，某市有一块长为米，宽为米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米？并求出当，时的绿化面积．

如图，一张长方形纸片宽AB＝8 cm，长BC＝10 cm．现将纸片折叠，使顶点D落在BC边上的点F处(折痕为AE)，求EC的长．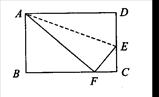

如图，在梯形ABCD中，AD∥BC， BC＝30cm，动点M从A点开始沿AD边向D以1cm/s的速度运动，动点N从C点开始沿CB边向B以3cm/s的速度运动，M、N分别从A、C同时出发，当其中一点到端点时，另一点也随之停止运动，设运动时间为t s，t为何值时，四边形ABNM是平行四边形？

如图，矩形ABCD中，对角线AC、BD交于点O，DE∥OC，CE∥OD，试判断四边形OCDE是何特殊四边形，并加以证明。

如图，ABCD是菱形，对角线AC与BD相交于O，∠ACD=30°，BD=6．
（1）求证：△ABD是正三角形；
（2）求AC的长（结果可保留根号）．

已知：如图，在平行四边形ABCD中，对角线AC、BD相交于点O，AE⊥BD，CF⊥BD，垂足分别为E、F．
求证：四边形AECF是平行四边形．

如图，在正方形ABCD中，CE⊥DF．若CE=10cm，求DF的长．