如图,ABMN中,AC平分∠BAN交BM于C点,CD∥AB交AN于D点.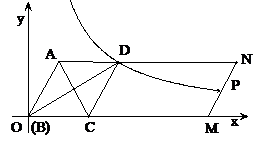
(1)判断四边形ABCD的形状并证明你的结论;
(2)以B点为坐标原点,BM所在的直线为横轴建立平面直角坐标系,若∠ABM = 60°,A点横坐标为2,请直接写出A、C、D点坐标及经过D点的反比例函数解析式;
(3)设(2)中反比例函数的图象与MN交于P点,求当BM的长为多少时,P点为MN的中点。
如图,点A在双曲线y=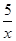 上,点B在双曲线y=
上,点B在双曲线y=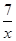 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为平行四边形,则它的面积为 .
上,且AB∥x轴,C、D在x轴上,若四边形ABCD为平行四边形,则它的面积为 .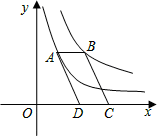
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标(4,2),过点D(0,3)和E(6,0)的直线分别于AB,BC交于点M,N.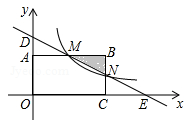
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数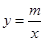 (x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
(x>0)的图象经过点M,求该反比函数的解析式,并通过计算判断点N是否在该函数的图象上.
如图,矩形OABC的顶点A,C的坐标分别是(4,0)(0,2),反比例函数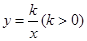 的图像过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则⊿ODE的面积为_____________.
的图像过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则⊿ODE的面积为_____________.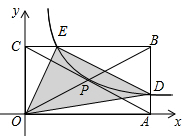
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线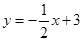 交AB,BC于点M,N,反比例函数
交AB,BC于点M,N,反比例函数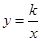 的图象经过点M,N.
的图象经过点M,N.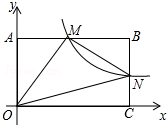
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
如图,已知点D在双曲线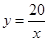 (
(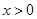 )的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线
)的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线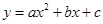 经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.
经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.
(1)写出点D的坐标并求出抛物线的解析式;
(2)证明∠ACO=∠OBC;
(3)探究是否存在点P,使点Q为线段AP的四等分点?若存在,求出点P的坐标;若不存在,请说明理由.
直线y=x+b与x轴交于点C(4,0),与y轴交于点B,并与双曲线y=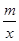 (x<0)交于点A(-1,n).
(x<0)交于点A(-1,n).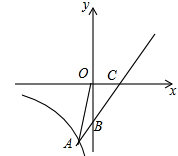
(1)求直线与双曲线的解析式.
(2)连接OA,求∠OAB的正弦值.
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由.
如图1,点A(1,6)和点M(m,n)都在反比例函数y= (k>0)的图象上.
(k>0)的图象上.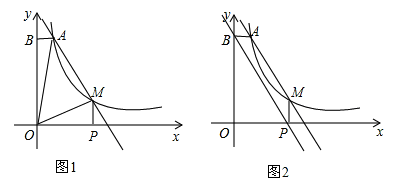
(1)求反比例函数的解析式;
(2)当m=3时,求直线AM的解析式,并求出△AOM的面积;
(3)如图2,当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.
如图,在平面直角坐标系中,四边形ABCD是菱形,B、O在x轴负半轴上,AO=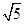 ,tan∠AOB=
,tan∠AOB=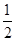 ,一次函数
,一次函数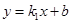 的图象过A、B两点,反比例函数
的图象过A、B两点,反比例函数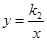 的图象过OA的中点D.
的图象过OA的中点D.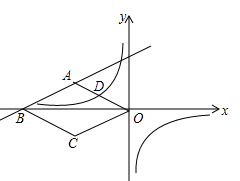
(1)求一次函数和反比例函数的表达式;
(2)平移一次函数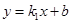 的图象,当一次函数
的图象,当一次函数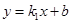 的图象与反比例函数
的图象与反比例函数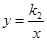 的图象无交点时,求b的取值范围.
的图象无交点时,求b的取值范围.
(本小题满分9分)如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).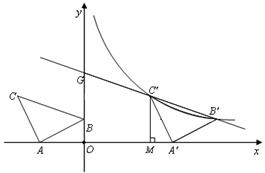
(1)求d的值;
(2)将△ABC沿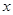 轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线
轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线 的解析式;
的解析式;
(3)在(2)的条件下,直线 交y轴于点G,作
交y轴于点G,作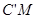 ⊥
⊥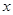 轴于
轴于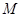 .
.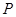 是线段
是线段 上的一点,若△
上的一点,若△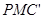 和△
和△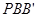 面积相等,求点
面积相等,求点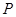 坐标.
坐标.
(黄石)已知双曲线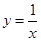 (
(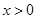 ),直线
),直线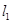 :
: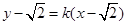 (
(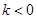 k<0)过定点F且与双曲线交于A,B两点,设A(
k<0)过定点F且与双曲线交于A,B两点,设A(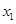 ,
,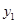 ),B(
),B(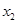 ,
, )(
)(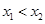 ),直线
),直线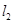 :
: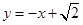 .
.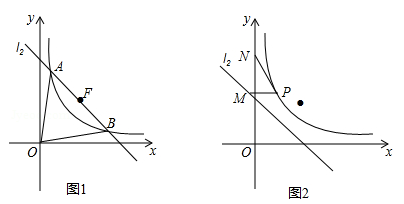
(1)若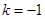 ,求△OAB的面积S;
,求△OAB的面积S;
(2)若AB=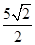 ,求k的值;
,求k的值;
(3)设N(0,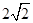 ),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.(参考公式:在平面直角坐标系中,若A(
),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.(参考公式:在平面直角坐标系中,若A(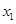 ,
,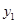 ),B(
),B(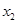 ,
, )则A,B两点间的距离为AB=
)则A,B两点间的距离为AB=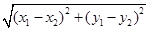 .
.
(本题2+3+3+4分)如图1,点A是反比例函数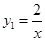 (x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数
(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数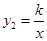 (k<0,x<0)的图象于点B.
(k<0,x<0)的图象于点B.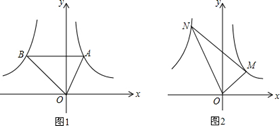
(1)若S△AOB=3,则k=______;
(2)当k=-8时:
①若点A的横坐标是1,求∠AOB的度数;
②将①中的∠AOB绕着点O旋转一定的角度,使∠AOB的两边分别交反比例函数y1、y2的图象于点M、N,如图2所示.在旋转的过程中,∠OMN的度数是否变化?并说明理由;
(3)如图1,若不论点A在何处,反比例函数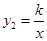 (k<0,x<0)图象上总存在一点D,使得四边形AOBD为平行四边形,求k的值.
(k<0,x<0)图象上总存在一点D,使得四边形AOBD为平行四边形,求k的值.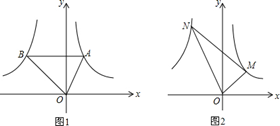
如图,一次函数y=kx+3的图象分别交x轴、y轴于点C、D两点,与反比例函数y=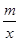 的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0, -6)且S△DBP=27.
的图象在第四象限相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0, -6)且S△DBP=27.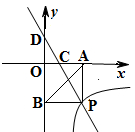
(1)求上述一次函数与反比例函数的表达式;
(2)设点Q是一次函数y=kx+3图象上的一点,且满足S△DOQ="2" S△COD,求点Q的坐标.
(本小题满分10分)已知A(-4,2),B(2,-4)是一次函数y=kx+b的图象和反比例函数 y =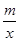 图象的两个交点.
图象的两个交点.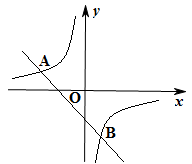
(1)求反比例函数和一次函数的表达式;
(2)将一次函数y=kx+b的图象沿y轴向上平移n个单位长度,交y轴于点C,若S△ABC=12,求n的值.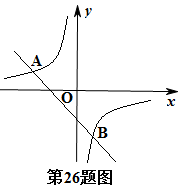
如图,直线 与反比例函数
与反比例函数 的图象在第一象限内交于A、B两点,交x轴的正半轴于C点,若AB:BC=(m-1):1(m>1),则△OAB的面积(用m表示)为( )
的图象在第一象限内交于A、B两点,交x轴的正半轴于C点,若AB:BC=(m-1):1(m>1),则△OAB的面积(用m表示)为( )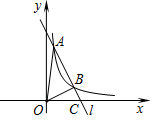
A.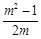 B.
B.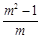 C.
C.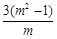 D.
D.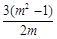
试题篮
()