已知反比例函数 和一次函数y=-x+a-1(a为常数)
和一次函数y=-x+a-1(a为常数)
(1)当a=5时,求反比例函数与一次函数的交点坐标
(2)是否存在实数a,使反比例函数与一次函数有且只有一个交点,如果存在,求出实数a,如果不存在,说明理由
如图,一次函数y=kx+b的图象与反比例函数y= 的图象交于A、B两点.
的图象交于A、B两点.
(1)利用图中的条件,求反比例函数和一次函数的解析式.
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
如图,在平面直角坐标系中,反比例函数 (
( >0)的图象和矩形ABCD的第一象限,AD平行于
>0)的图象和矩形ABCD的第一象限,AD平行于 轴,且AB=2,AD=4,点A的坐标为(2,6).
轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
如图,已知反比例函数 与一次函数
与一次函数 的图象在第一象限相交于点A(1,
的图象在第一象限相交于点A(1, )
)
(1)试确定这两个函数的表达式;
(2)求出这两个函数图像的另一个交点B的坐标,并根据图象写出使一次函数的值小于反比例函数值的x的取值范围.
如图,已知直线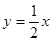 与双曲线
与双曲线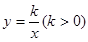 交于
交于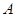 、
、 两点,
两点, 点横坐标为4.
点横坐标为4.
(1)求 值;
值;
(2)直接写出关于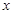 的不等式
的不等式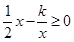 的解集;
的解集;
(3)若双曲线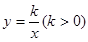 上有一点
上有一点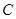 的纵坐标为8,求△
的纵坐标为8,求△ 的面积.
的面积.
(4)若在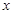 轴上有点
轴上有点 ,
,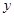 轴上有点
轴上有点 ,且点
,且点 、
、 、
、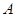 、
、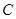 四点恰好构成平行四边形,直接写出点
四点恰好构成平行四边形,直接写出点 、
、 的坐标.
的坐标.
某生态示范村种植基地计划用90亩~120亩的土地种植一批葡萄,原计划总产量要达到36万斤.
(1)列出原计划种植亩数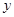 (亩)与平均每亩产量
(亩)与平均每亩产量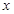 (万斤)之间的函数关系式,并写出自变量
(万斤)之间的函数关系式,并写出自变量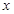 的取值范围;(总产量=亩数
的取值范围;(总产量=亩数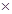 平均每亩产量)
平均每亩产量)
(2)为了满足市场需求,现决定改良葡萄品种.改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了8万斤,种植亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?
实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x (时)的关系可近似地用二次函数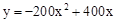 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数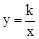 (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当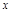 =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.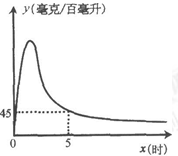
如图,已知A ,B(-1,2)是一次函数
,B(-1,2)是一次函数 与反比例函数
与反比例函数
( )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。
)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标。
如图,反比例函数 的图象与一次函数
的图象与一次函数 的图象交于点A(m,2),点B(-2, n ),一次函数图象与y轴的交点为C.求△AOC的面积。
的图象交于点A(m,2),点B(-2, n ),一次函数图象与y轴的交点为C.求△AOC的面积。
如图所示,在平面直角坐标系中,一次函数y=kx+1,的图象与反比例函数 的图象在第一象限相交于点A,过点A分别作x 轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.
的图象在第一象限相交于点A,过点A分别作x 轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.
如图,一条直线与反比例函数 的图象交于A(1,4)
的图象交于A(1,4)
B(4,n)两点,与 轴交于D点,AC⊥
轴交于D点,AC⊥ 轴,垂足为C.
轴,垂足为C.
(1)如图甲,①求反比例函数的解析式;②求n的值及D点坐标;
(2)如图乙,若点E在线段AD上运动,连结CE,作∠CEF=45°,EF交AC于F点.
①试说明△CDE∽△EAF;
②当△ECF为等腰三角形时,直接写出F点坐标 .
如图,已知反比例函数 (
( )的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥
)的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥ 轴,AC=1(点C位于点A的下方),过点C作CD∥
轴,AC=1(点C位于点A的下方),过点C作CD∥ 轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC、OD.
轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC、OD.
(1)求该反比例函数的解析式;
(2)求△OCD的周长;
(3)若BE= AC,求CE的长.
AC,求CE的长.
已知双曲线y= (k>0),过点M(m,m)(m>
(k>0),过点M(m,m)(m> )作MA⊥x轴,MB⊥y轴,垂足分别是A和B,MA、MB分别交双曲线y=
)作MA⊥x轴,MB⊥y轴,垂足分别是A和B,MA、MB分别交双曲线y= (k>0)于点E、F。
(k>0)于点E、F。
(1)若k=2,m=3,求直线EF的解析式;
(2)O为坐标原点,连接OF,若∠BOF=22.5°,多边形BOAEF的面积是2,求k值。
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.
(1)求k和b的值;
(2)求△OAB的面积.
试题篮
()