如图,一次函数的图象与反比例函数y1=- (x<0)的图象相交于正A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<-1时,一次函数值大于反比例函数值;当x>-1时,一次函数值小于反比例函数值
(x<0)的图象相交于正A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<-1时,一次函数值大于反比例函数值;当x>-1时,一次函数值小于反比例函数值
(1)求一次函数的解析式
(2)设函数y2= (x>0)的图象与y1=-
(x>0)的图象与y1=- (x<0)的图象关于y轴对称,在y2=
(x<0)的图象关于y轴对称,在y2= (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标
(x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标
如图,一次函数y=﹣x+2的图象与反比例函数y=﹣ 的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.
的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.
(1)求A、B两点的坐标;
(2)求△ABC的面积.
如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y= (x>0)的图象经过矩形的对称中心E,且与边BC交于点 D.
(x>0)的图象经过矩形的对称中心E,且与边BC交于点 D.
(1)求反比例函数的解析式和点D的坐标;
(2)若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,求此直线的解析式.
如图,直线L:y=﹣x+3与两坐标轴分别相交于点A、B.
(1)当反比例函数y= (m>0,x>0)的图象在第一象限内与直线L至少有一个交点时,求m的取值范围.
(m>0,x>0)的图象在第一象限内与直线L至少有一个交点时,求m的取值范围.
(2若反比例函数y= (m>0,x>0)在第一象限内与直线L相交于点C、D,当CD=
(m>0,x>0)在第一象限内与直线L相交于点C、D,当CD= 时,求m的值.
时,求m的值.
(3)在(2)的条件下,请你直接写出关于x的不等式﹣x+3< 的解集.
的解集.
如图,将透明三角形纸片PAB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数 图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).
图象的两支上,且PB⊥x于点C,PA⊥y于点D,AB分别与x轴,y轴相交于点E、F.已知B(1,3).
(1)k= ;
(2)试说明AE=BF;
(3)当四边形ABCD的面积为 时,求点P的坐标.
时,求点P的坐标.
如图,一次函数y=kx+b的图象与坐标轴分别交于A,B两点,与反比例函数y= 的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
(1)求一次函数与反比例的解析式;
(2)直接写出当x<0时,kx+b﹣ >0的解集.
>0的解集.
如图,已知函数 (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE=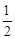 AC时,求CE的长.
AC时,求CE的长.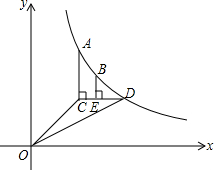
如图,经过原点的两条直线 、
、 分别与双曲线
分别与双曲线 相交于A、B、P、Q四点,其中A、P两点在第一象限,设A点坐标为(3,1).
相交于A、B、P、Q四点,其中A、P两点在第一象限,设A点坐标为(3,1).
(1)求 值及
值及 点坐标;
点坐标;
(2)若P点坐标为(a,3),求a值及四边形APBQ的面积;
(3)若P点坐标为(m,n),且 ,求P点坐标.
,求P点坐标.
已知 ,
, 与
与 成反比例,
成反比例, 与
与 成正比例,并且当
成正比例,并且当 时,
时, ,当
,当 时,
时,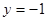 .
.
(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)当 时,求
时,求 的值.
的值.
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y= 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
(1)求反比例函数解析式;
(2)求点C的坐标.
如图,在边为的1正方形组成的网格中,建立平面直角坐标系,若A(﹣4,2)、B(﹣2,3)、C(﹣1,1),将△ABC沿着x轴翻折后,得到△DEF,点B的对称点是点E,求过点E的反比例函数解析式,并写出第三象限内该反比例函数图象所经过的所有格点的坐标.
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y= (x>0)的函数图象经过点D,点P是一次函数
(x>0)的函数图象经过点D,点P是一次函数
 的图象与该反比例函数图象的一个公共点.
的图象与该反比例函数图象的一个公共点.
(1)求反比例函数的解析式;
(2)通过计算,说明一次函数
 的图象一定过点C;
的图象一定过点C;
(3)对于一次函数
 ,当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).
,当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y=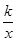 (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是OC边上一点,且△FBC∽△DEB,求直线FB的解析式.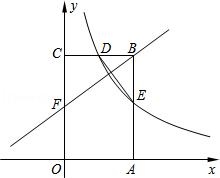
已知直线l平行于直线y=2x+1,并与反比例函数 的图象相交于点A(a,1),求直线l的解析式.
的图象相交于点A(a,1),求直线l的解析式.
试题篮
()