初中数学平行线分线段成比例解答题

（本小题8分）已知反比例函数的图象经过点A（1，3）.
求：（Ⅰ）m的值和这个函数的解析式；
（Ⅱ）当-3＜＜-1时，对应的函数的取值范围.

已知B（2，n）是正比例函数y=2x图象上的点．
（1）求点B的坐标；
（2）若某个反比例函数图象经过点B，求这个反比例函数的解析式．

直线y=―x―2与反比例函数y=的图像交于Ａ、Ｂ两点，且与x、y轴交于C、D两点，A点的坐标为（－3，k＋4）.
（1）求反比例函数的解析式
（2）把直线AB绕着点M（―1，―1）顺时针旋转到MN，使直线MN⊥x轴，且与反比例函数的图像交于点N，求旋转角大小及线段MN的长。

（11·肇庆）(本小题满分8分)如图9．一次函数y＝x＋b的图象经过点B (－1，0)，且与反比例函数 (k为不等于0的常数)的图象在第一象限交于点A (1，n)．求：
（1）一次函数和反比例函数的解析式；
（2）当1≤x≤6时，反比例函数y的取值范围．

(10分)如图，已知一次函数y＝kx＋b的图象交反比例函数的
图象于点A、B，交x轴于点C．
(1)求m的取值范围；
(2)若点A的坐标是(2，－4)，且，求m的值和一次函数的解析式．

如图，点D在双曲线上，AD垂直轴，垂足为
A，点C在AD上，CB平行于轴交双曲线于点B，直线AB与轴交于点F，已知AC：
AD=1：3，点C的坐标为（2，2）。
（1）求该双曲线的解析式；
（2）求△OFA的面积。

(8分)如图，矩形ABCD中，AB＝1，BC＝2，BC在x轴上，一次函数y＝kx
－2的图象经过点A、C，并与y轴交于点E，反比例函数的图象经过点A．
(1)点E的坐标是           ；
(2)求一次函数和反比例函数的解析式；
(3)根据图象写出当x＞0时，一次函数的值大于反比例函数的值的x的取值范围．

(本题满分7分.)如图7,反比例函数的图像与一次函数的图象交于点A、B,其中A(1,2)．

(1)求m，b的值；
(2)求点B的坐标,并写出时，的取值范围．   

（11·钦州）
如图，在平面直角坐标系中，点O为原点，反比例函数y＝的图象经过点(1，4)，菱形OABC的顶点A在函数的图象上，对角线OB在x轴上．
（1）求反比例函数的关系式；
（2）直接写出菱形OABC的面积．

（11·柳州）
如图，直线y＝kx＋k（k≠0）与双曲线在第一象限内相交于点M，与x轴交于点A．
（1）求m的取值范围和点A的坐标；
（2）若点B的坐标为（3，0），AM＝5，S_△ABM＝8，求双曲线的函数表达式．

如图，已知直线AB与x轴交于点C，与双曲线交于A（3，）、B（﹣5，a）两点．AD⊥x轴于点D，BE∥x轴且与y轴交于点E．
（1）求点B的坐标及直线AB的解析式；
（2）判断四边形CBED的形状，并说明理由．

如图，四边形ABCD为菱形,已知A(0,4)，B(－3,0).

（1）求点D的坐标；
（2）求经过点C的反比例函数解析式.

(本题6分) (湖南湘西,22,6分)如图,已知反比例函数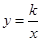的图象经过点A(1,2).

(1)求k的值.
(2)过点A分别作x轴和y轴的垂线,垂足为B和C,求矩形ABOC的面积.

如图，已知反比例函数的图像经过第二象限内的点A（－1，m），AB⊥x轴于点B，△AOB的面积为2．若直线y=ax+b经过点A，并且经过反比例函数的图象上另一点C（n，一2）．
⑴求直线y=ax+b的解析式；
⑵设直线y=ax+b与x轴交于点M，求AM的长．