初中数学平行线分线段成比例解答题

如图，为双曲线上一点，直线平行于轴交直线于点，求（OB+AB）(OB-AB)的值

如图，平行于y轴的直尺（一部分）与双曲线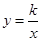（x＞0）交于点A、C，与x轴交于点B、D，连结AC．点A、B的刻度分别为5、2（单位：cm），直尺的宽度为2cm，OB=2 cm．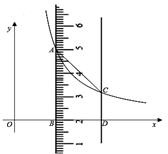

(1)求k的值；
(2)求经过A、C两点的直线解析式.

已知图中的曲线是反比例函数（为常数）图象的一支．

（1）这个反比例函数图象的另一支在第几象限？常数的取值范围是什么？
（2）若该函数的图象与正比例函数的图象在第一象内限的交点为，过点作轴的垂线，垂足为，当的面积为4时，求点的坐标及反比例函数的解析式．

如图所示，已知一次函数与反比例函数的图象交于A(-4,-2)和B（，4）.

（1）求反比例函数的解析式和点B的坐标；
（2）根据图象直接写出，当在什么范围内时，一次函数的值大于反比例函数的值？

如图1，已知双曲线与直线交于A,B两点，点A的坐标为（3，1）.试解答下列问题:


⑴求点B的坐标；
⑵当x满足什么范围时，；
⑶过原点O作另一条直线l，交双曲线于P,Q两点，点P在第一象限， 如图2所示.
① 试判断四边形APBQ的形状，并加以说明；
② 若点P的横坐标为1，求四边形APBQ的面积；

如图，在平面直角坐标系xOy中，一次函数y＝－2x的图象与反比例函数y＝的图象的一个交点为A(－1，n)．

(1)求反比例函数y＝的解析式；
(2)若P是坐标轴上一点（P点不与O点重合），且满足PA＝OA，直接写出点P的坐标．

已知正比例函数y＝4x的图像与反比例函数y（k≠0）在第一象限的图像交于A点，过A点作x轴的垂线，垂足为P点，已知△OAP的面积为

（1）求反比例函数的解析式；
（2）如果点B为反比例函数在第一象限图象上的点（点B与点A不重合），且点B的横坐标为1，在x轴上求一点M，使MA＋MB最小。

已知，如图：点A（，1）在反比例函数图象上，将y轴绕点O顺时针旋转30°，与反比例函数在第一象限内交于点B，

求:（1）反比例函数的解析式；
（2）求点B的坐标及△AOB的面积．

装卸工人往一辆大型运货车上装载货物．装完货物所需时间（min）与装载速度（t/min）之间的函数关系如图：

（1）这批货物的质量是多少？
（2）写出与之间的函数关系式；
（3）货车到达目的地后开始卸货，如果以1.5t/min的速度卸货，需要多长时间才能卸完货物？

如图，一次函数的图像与反比例函数的图像相交于A、B两点，

（1）利用图中条件，求反比例函数和一次函数的解析式
（2）根据图像写出使一次函数的值大于反比例函数的值的的取值范围

一次函数的图象与反比例函数＝（＞0）的图象交于、两点，与轴交于点，已知点坐标为（2，1），点坐标为（0，3）. 求函数的表达式和点的坐标。

如图，已知A（－4，n）、B（2，－6）是一次函数y₁＝k₁x＋b与反比例函数y₂＝的两个交点，直线AB与x轴交于点C。

（1）求两函数解析式；
（2）求△AOB的面积；
（3）根据图象回答：当x＞－4时，反比例函数y₂的函数值的取值范围；
（4）根据图象回答：y₁＜y₂时，自变量x的取值范围。

2013年4月20日8时2分在四川省雅安市芦山县发生7.0级地震，震源深度13千米。某粮食公司接到救灾任务，要将2400吨粮食调往灾区。
（1）调运所需天数t（天）与调运速度v（吨/天）有怎样的函数关系？
（2）如果调用20辆汽车，每辆汽车每天可调运6吨，预计这批粮食最快在几天内全部运到灾区？
（3）当这20辆汽车工作4天后，公司接到救灾指挥部的指示，要求在4天内把剩下的粮食全部运往灾区，这时公司需要增派多少辆同样的汽车才能完成任务？

如图，在以O为原点的直角坐标系中，点A、C分别在x轴、y轴的正半轴上，点B（a，b）在第一象限，四边形OABC是矩形，若反比例函数（k＞0，x＞0）的图象与AB相交于点D，与BC相交于点E，且BE=CE.

（1）求证：BD=AD；
（2）若四边形ODBE的面积是9，求k的值.

已知y=y₁+y₂，其中y₁与x成反比例，y₂与(x-2)成正比例.当x=1时，y=-1；x=3时，y=3.
（1）求y与x的函数关系式；   （2）当x=-1时，y的值。