已知:如图,正比例函数y=ax的图象与反比例函数y= 的图象交于点A(3,2).
的图象交于点A(3,2).
(1)确定上述正比例函数和反比例函数的表达式
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)M(m,n)是反比例函数图象上的一个动点,其中0<m<3,过点M作直线MB//x轴,交y轴于点B;过点A作直线AC//y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为3时,请判断线段BM与DM有何数量关系,并说明理由.
如图,已知A(4,a),B(-2,-4)是一次函数y=k x+b 的图象和反比例函数 的图象的交点.
的图象的交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
(3)根据图象求出使一次函数的值大于反比例函数的值时,x的取值范围.
如图,反比例函数 与一次函数
与一次函数 的图像交于两点A(
的图像交于两点A( ,-1)、B(1,2).
,-1)、B(1,2).
(1)求反比例函数与一次函数的关系式;
(2)根据图象,直接回答:当 取何值时,
取何值时, ≥
≥ ?
?
(3)连接OA、OB,求△AOB的面积;
(4)在反比例函数的图象上找点P,使△POB为等腰三角形,这样的P点有几个?
并直接写出两个满足条件的点P的坐标.
码头工人往一艘轮船上装载货物.装完货物所需时间 与装载速度
与装载速度 之间的函数关系如图:
之间的函数关系如图:
(1)这批货物的质量是多少?
(2)写出 与
与 之间的函数关系式;
之间的函数关系式;
(3)轮船到达目的地后开始卸货,如果要在2小时内
将货物卸完,则卸货速度至少为每分钟多少吨?
如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C坐标为(-1,0), .一次函数
.一次函数 的图象经过点B、C,反比例函数
的图象经过点B、C,反比例函数 的图象经过点B.
的图象经过点B.
(1)求一次函数和反比例函数的关系式;
(2)直接写出当x<0时, 的解集;
的解集;
(3)在 轴上找一点M,使得AM+BM的值最小,并求出点M的坐标和AM+BM的最小值.
轴上找一点M,使得AM+BM的值最小,并求出点M的坐标和AM+BM的最小值.
如图,已知一次函数 的图象与反比例函数
的图象与反比例函数 的图象交与A(2,4)和B(-4,m)两点.
的图象交与A(2,4)和B(-4,m)两点.
(1)求这两个函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出,当 时,x的取值范围.
时,x的取值范围.
已知一次函数y1=ax+b的图象与反比例函数y2= 的图象相交于A、B两点,坐标分别为(—2,4)、(4,—2)。
的图象相交于A、B两点,坐标分别为(—2,4)、(4,—2)。
(1)求两个函数的解析式;
(2)求△AOB的面积;
(3)直线AB上是否存在一点P(A除外),使△ABO与以B﹑P、O为顶点的三角形相似?若存在,直接写出顶点P的坐标。
如图1,在平面直角坐标系中,点A、C分别在 轴、
轴、 轴上,四边形OABC是面积为4的正方形,函数
轴上,四边形OABC是面积为4的正方形,函数 (
( >0)的图象经过点B.
>0)的图象经过点B.
(1) = ;
= ;
(2)如图2,将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′和正方形MA′BC.设线段MC′、NA′分别与函数 (
( >0)的图象交于点E、F,则点E、F的坐标分别为:E ( , ) ,F ( , );
>0)的图象交于点E、F,则点E、F的坐标分别为:E ( , ) ,F ( , );
(3)如图3,面积为4的正方形ABCD的顶点A、B分别在 轴、
轴、 轴上,顶点C、D在反比例函数
轴上,顶点C、D在反比例函数 (
( >0)的图像上,试求OA、OB的长。(请写出必要的解题过程)
>0)的图像上,试求OA、OB的长。(请写出必要的解题过程)


一辆汽车匀速通过某段公路,所需时间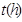 与行驶速度
与行驶速度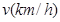 满足函数关系:
满足函数关系: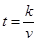 ,其图象为如图所示的一段曲线且端点为A(20,1)和B(
,其图象为如图所示的一段曲线且端点为A(20,1)和B( ,0.5).
,0.5). 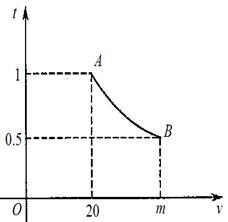
(1)求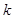 和
和 的值;
的值;
(2)若行驶速度不得超过60 km/h,则汽车通过该路段最少需要多少时间 ?
如图,已知函数 与
与 相交于A,B两点,且A(3,4)过A作AC⊥x轴于C点,
相交于A,B两点,且A(3,4)过A作AC⊥x轴于C点,
(1)求反比例函数的关系式.
(2)观察图象,当x在什么范围内时正比例函数值大于反比例函数的值.
(3)在坐标轴上是否存在一点E使得以B,O,E为顶点的三角形与△AOC相似(三角形全等除外)? 若存在,求出E点坐标;若不存在,请说明理由.
如图,反比例函数 (
( )与长方形
)与长方形 在第一象限相交于
在第一象限相交于 、
、 两点,
两点, ,
, ,连结
,连结 、
、 、
、 .记
.记 、
、 的面积分别为
的面积分别为 、
、 .
.
(Ⅰ)①点 坐标为 ;②
坐标为 ;②
 (填“>”、“<”、“=”);
(填“>”、“<”、“=”);
(Ⅱ)当点 为线段
为线段 的中点时,求
的中点时,求 的值及点
的值及点 坐标;
坐标;
(Ⅲ)当 时,试判断
时,试判断 的形状 ,并求
的形状 ,并求 的面积.
的面积.
如图,直线y=kx+b与反比例函数 只有一个交点A(1 , 2),且与x轴、y轴分别交于B,C两点,AD垂直平分OB,垂足为D,
只有一个交点A(1 , 2),且与x轴、y轴分别交于B,C两点,AD垂直平分OB,垂足为D,
(1)求点B的坐标和m的值;
(2)求直线解析式
如图,已知A(-4,2)、B(n,-4)是一次函数 的图象与反比例函数
的图象与反比例函数 的图象的两个交点.
的图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)求△ABO的面积。
试题篮
()