初中数学平行线分线段成比例解答题

如图，在直角坐标系中，点是反比例函数的图象上一点，轴的正半轴于点，是的中点；一次函数的图象经过、两点，并交轴于点若

（1）求反比例函数和一次函数的解析式；
（2）观察图象，请写出在轴的右侧，当时，的取值范围．

如图，已知A，B两点的坐标分别为A(0，2)，B(2，0)直线AB与反比例函数的图像交与点C和点D（－1，）．

(1)求直线AB和反比例函数的解析式；
(2)求∠ACO的度数；
(3)将△OBC绕点O逆时针方向旋转α角（α为锐角），得到△OB′C′，当α为多少度时OC′⊥AB，并求此时线段AB′的长．

如图，反比例函数y=（k≠0）的图象经过点（－2，8）．

（1）求这个反比例函数的解析式；
（2）若（2，y₁），（4，y₂）是这个反比例函数图象上的两个点，请比较y₁，y₂的大小，并说明理由．

如图，在直角坐标系xOy中，直线与双曲线相交于A（－1，a）、B两点，BC⊥x轴，垂足为C，△AOC的面积是1．

（1）求m、n的值；
（2）求直线AC的解析式．

直线y=－x+b与双曲线相交于点D(－4，1)、C(1，m)，并分别与坐标轴交于A、B两点，过点C作直线MN⊥x轴于F点，连接BF．

（1）求直线和双曲线的解析式；
（2）作出△ABF的外接圆，并求出圆心I的坐标；
（3）在（2）中⊙I与直线MN的另一交点为E，判断点D、I、E是否共线？说明理由.

如图,Rt△ABO的顶点A是双曲线y=与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且.(1)求这两个函数的解析式;(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出：(3)方程的解；(4)使一次函数的值大于反比例函数的值的的取值范围；

已知一次函数y=ax＋b的图像与反比例函数 的图像交于A（2，2），B(－1，m)，求反比例函数和一次函数的解析式．

如图，在平面直角坐标系中，四边形ABCD为矩形，BC平行于x轴，AB＝6，点A的横坐标为2，反比例函数y＝的图像经过点A、C．

（1）求点A的坐标；
（2）求经过点A、C所在直线的函数关系式．
（3）请直接写出AD长    ．

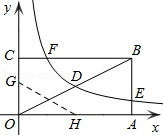
如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数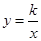（k≠0）在第一象限内的图象经过点D、E，且tan ∠ BOA=．

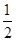（1）求边AB的长；
（2）求反比例函数的解析式和n的值；
（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求线段OG的长．

如图：一次函数y=kx+b的图象与反比例函数y=的图象相交于A(－2，1)、B(1、n)两点。

（1）求一次函数和反比例函数的解析式；
（2）求△AOB的面积；
（3）当x为何值时，一次函数的值大于反比例函数的值？
（直接写出答案）

已知反比例函数y=与一次函数y=mx+b的图象交于P(－2，1)和Q（1，n）两点．
（1）求k、n的值；
（2）求一次函数y=mx+b的解析式；
（3）求△POQ的面积．

如图，在平面直角坐标系xOy中，直线的图象与反比例函数的图象交于点A(1，m)，与x轴交于点，过点A作轴于点．

（1）求一次函数的解析式；
（2）若P为x轴上一点，且△ABP的面积为10，直接写出点的坐标．

如图所示制作一种产品，需先将材料加热达到60℃后，再进行操作。设该材料温度为y（℃），从加热开始计算的时间为x（min）。据了解，设该材料开始加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y 与时间x成反比例关系（如图）。已知该材料在操作加工前的温度为20℃，加热5分钟后温度达到60℃。

（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式。   
（2）根据工艺要求，是材料的温度低于15℃，需停止操作，那么从开始加热到停止操作，共经历了多少时间。

如图，直线与双曲线交于点A、B两点，且点A的横坐标为4，

（1）求k的值，
（2）若双曲线上一点C的纵坐标为1，过点C作CD垂直x轴于点D，求△AOD的面积.

如图，反比例函数 y＝的图象与一次函数y＝mx＋b的图象交于两点A（1，3）、B（n，－1）

（1）求反比例函数与一次函数的函数关系式；
（2）根据图象，直接回答：当x取何值时，一次函数的值大于反比例函数的值；
（3）连接AO、BO，求△AOB的面积。