初中数学平行线分线段成比例解答题

已知直线y₁=x+m与x轴、 y轴分别交于点A、B,与双曲线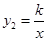(x＜0)分别交于点C、D,且C点的坐标为(-1，2).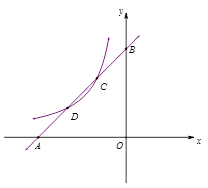

(1)分别求出直线AB及双曲线的解析式；
(2)求出点D的坐标；
(3)在坐标轴上找一点M,使得以M、C、D为顶点的三角形是直角三角形,请直接写出M点坐标.

如图，已知一次函数与反比例函数的图象交于A、B两点．

（1）求A、B两点的坐标；
（2）如果，根据图象直接写出的取值范围．

如图，函数的图象与函数（）的图象交于A（a，1）、B（1，b）两点．

（1）求k的值；
（2）设y₁=-x+4，，利用图象分别写出x＞1时y₁和y₂的取值范围，以及y₁与y₂的大小关系．

如图所示，四边形ABCD为正方形．点A的坐标为（0，2），点B的坐标为（0，－3），反比例函数y＝的图象经过点C，一次函数y＝ax＋b的图象经过点C，点A．

（1）求反比例函数与一次函数的解析式；
（2）点P是反比例函数图象上的一点，△OAP的面积恰好等于正方形ABCD的面积，求P点的坐标．

如图，一次函数y＝x＋6与反比例函数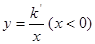的图象相交于A，B两点，与x轴、y轴交于E、F，点B的横坐标为。

（1）试确定反比例函数的解析式；
（2）求点E、F的坐标。

（本小题满分12分）如图，在平面直角坐标系xOy中，若点A（－2，n），B（1，－2）是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点．

（1）求反比例函数和一次函数的解析式；
（2）求直线AB与x轴的交点C的坐标；
（3）求点到直线AB的距离．

如图，在直角梯形OABC中，BC∥AO，∠AOC=90°，点A，B的坐标分别为（5，0），（2，6），点D为AB上一点，且BD=2AD，曲线（k＞0）经过点D，交BC于点E．

（1）求曲线的解析式；
（2）求四边形ODBE的面积．

如图，A、B是双曲线上的点，点A的坐标是（1，4），B是线段AC的中点．

（1）求k的值；
（2）求△OAC的面积．

已知一次函数与反比例函数的图象交于A（2，3）， B（-6，n） 两点．
（1）求一次函数和反比例函数的解析式；
（2）P是y轴上一点，且，直接写出P点坐标．

如图，直线y=mx与双曲线y=相交于A、B两点，A点的坐标为（1，2）

（1）求反比例函数的表达式
（2）根据图象直接写出当mx＞时，x的取值范围；
（3）计算线段AB的长．

问题1：在图1中，已知线段AB，CD，它们的中点分别为E，F．
①若，，则点坐标为_____________；
②若，，则点坐标为____________；
问题2：在图2中，无论线段处于直角坐标系中的哪个位置，当其端点坐标为，，中
点为时，请直接写出点的坐标（____________，___________）；（用含、、、的式子表示）．
问题3：如图3，一次函数与反比例函数的图象交于、两点，若以、、、为顶
点的四边形是平行四边形，请直接写出顶点的坐标______________．

（本题10分）如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，反比例函数在第一象限内的图象经过点D，与AB相交于点E，且点B（4，2）．

（1）求反比例函数的关系式；
（2）求四边形OAED的面积；
（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，若，求直线GH的函数关系式．

已知，如图，反比例函数的图像与一次函数的图像相交于点、，

（1）试确定这两个函数的表达式；
（2）求的面积；
（3）直接写出使反比例函数的值大于一次函数的值的的取值范围．

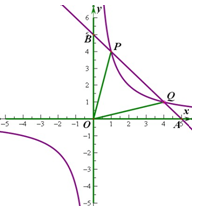
如图，已知反比例函数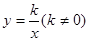的图象经过点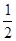（，8），直线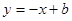经过该反比例函数图象上的点Q（4，）．

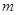（1）求上述反比例函数和直线的函数表达式；
（2）设该直线与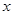轴、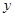轴分别相交于A 、B两点，与反比例函数图象的另一个交点为P，连结0P、OQ，求△OPQ的面积．

（10’）设x_i（i=1，2，3， ，n）为任意代数式，我们规定：y=max{x₁，x₂，x₃，…，x_n}表示x₁，x₂，…，x_n中的最大值，如y=max{1，2}=2．
（1）求y=max{x，3}；
（2）借助函数图象，解决以下问题：
①解不等式 max{x+1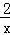，}≥2；
②若函数y=max{|x﹣1|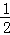，x+a，x²﹣4x+3}的最小值为1，求实数a的值．