初中数学平行线分线段成比例解答题

如图，在平面直角坐标系中，Rt△PBD的斜边PB落在y轴上，
tan∠BPD＝．延长BD交轴于点C，过点D作DA⊥轴，垂足为A，PD与轴交于点E，OA=8，OB=6．

（1）求点C的坐标；
（2）若点D在反比例函数y =（k＞0）的图象上，求反比例函数的解析式．

在直角坐标系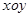中，已知点P是反比例函数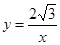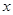（＞0）图象上一个动点，以P为圆心的圆始终与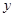轴相切，设切点为A．
（1）如图1，⊙P运动到与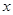轴相切，设切点为K，试判断四边形OKPA的形状，并说明理由．
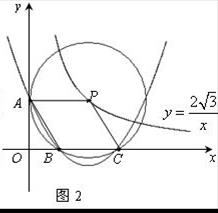
（2）如图2，⊙P运动到与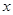轴相交，设交点为B，C．当四边形ABCP是菱形时：
①求出点A，B，C的坐标．
②在过A，B，C三点的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的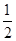．若存在，试求出所有满足条件的M点的坐标，若不存在，试说明理由．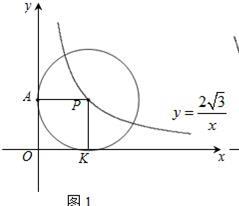
            

(8分）如图，四边形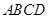是平行四边形，点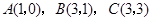．反比例函数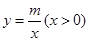的图象经过点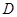，点是一次函数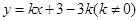的图象与该反比例函数图象的一个公共点．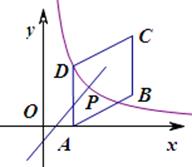

（1）求反比例函数的解析式；
（2）通过计算，说明一次函数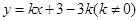的图象一定过点；
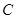（3）对于一次函数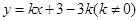，当的增大而增大时，确定点横坐标的取值范围（不写过程，直接写出结果）．

如图，在平面直角坐标系中，点A在第一象限，AB⊥x轴，B（2，0），tan∠AOB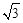＝，过点A的双曲线为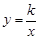，在x轴上取一点P，过点P作直线OA的垂线l，以直线l为对称轴，线段OB经轴对称变换后的对应线段O'B'．

（1）当点O'与点A重合时，求直线l的解析式：
（2）当点B'落在双曲线上时，求出点P的坐标．

如图，反比例函数（k为常数，且k≠5）经过点A（1，3）．

（1）求反比例函数的解析式；
（2）在x轴正半轴上有一点B，若△AOB的面积为6，求直线AB的解析式．

如图，直线y=﹣x+3与x，y轴分别交于点A，B，与反比例函数的图象交于点P（2，1）．

（1）求该反比例函数的关系式；
（2）设PC⊥y轴于点C，点A关于y轴的对称点为A′；
①求△A′BC的周长和sin∠BA′C的值；
②对大于1的常数m，求x轴上的点M的坐标，使得sin∠BMC=．

已知反比例函数y= （k≠0）的图象经过点（3，2）．
（1）求这个函数的解析式；
（2）当－4＜x＜－1时，求y的取值范围．

如图，在平面直角坐标系中，反比例函数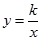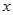（＞0）的图象和矩形ABCD的第一象限，AD平行于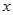轴，且AB＝2，AD＝4，点A的坐标为（2，6） ．

（1）直接写出B、C、D三点的坐标；
（2）若将矩形向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，猜想这是哪两个点，并求矩形的平移距离和反比例函数的解析式．

如图，一次函数y=kx+b与反比例函数的图象交于A（m，6），B（3，n）两点．

（1）求一次函数的解析式；
（2）根据图象直接写出的x的取值范围；
（3）求△AOB的面积．

在平面直角坐标系中，过点向轴作垂线，垂足为，连接．双曲线经过斜边的中点，与边交于点．

（1）求反比例函数的解析式；
（2）求△的面积．

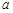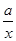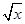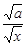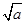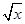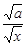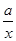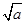（本题12分）阅读理解：配方法是中学数学的重要方法，用配方法可求最大（小）值。如对于任意正实数、x，可作变形：x+=（－）²+2，因为（－）²≥0，所以x+≥2（当x=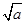时取等号）．
记函数y=x+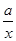（a＞0，x＞0），由上述结论可知：当x=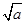时，该函数有最小值为2．
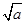直接应用： 已知函数y₁=x（x＞0）与函数y₂ = 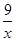（x＞0），则当x=         时，y₁+y₂取得最小值为      ．
变形应用： 已知函数y₁=x+1（x＞-1）与函数y₂=（x+1）²+4（x＞-1），求 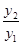的最小值，并指出取得该最小值时相应的x的值．
实际应用：汽车的经济时速是指汽车最省油的行驶速度。某种汽车在每小时70～110公里之间行驶时（含70公里和110公里），每公里耗油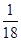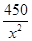（+）升。若该汽车以每小时x公里的速度匀速行驶，1小时的耗油量为y升．
①求y关于x的函数关系式（写出自变量x的取值范围）；
②求该汽车的经济时速及经济时速的百公里耗油量（结果保留小数点后一位）．

如图，已知直线y=4-x与反比例函数y=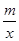（m>0,x>0）的图象交于A、B两点，与x轴、y轴分别相交于C、D两点．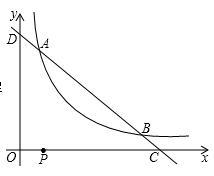

（1）如果点A的横坐标为1，利用函数图象求关于x的不等式4-x<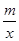的解集；
（2）如果点A的横坐标仍然为1，是否存在以AB为直径的圆经过点P（1,0）？若存在，求出m的值；若不存在，请说明理由．

某车队要把4000吨货物运到雅安地震灾区（方案定后，每天的运量不变）。
（1）从运输开始，每天运输的货物吨数n（单位：吨）与运输时间t（单位：天）之间有怎样的函数关系式？
（2）因地震，到灾区的道路受阻，实际每天比原计划少运20%，则推迟1天完成任务，求原计划完成任务的天数。

如图，一次函数y=kx+b的图象与坐标轴分别交于点E、F，与双曲线交于点P（-1，n），且F是PE的中点．

（1）求直线的解析式；
（2）若直线x=a与交于点A，与双曲线交于点B（不同于A），问a为何值时，PA=PB？

如图，在平面直角坐标系xOy中，矩形OABC的顶点A在x轴上，顶点C在y轴上，D是BC的中点，过点D的反比例函数图象交AB于E点，连接DE。若OD=5，tan∠COD=。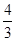

（1）求过点D的反比例函数的解析式；
（2）求△DBE的面积；
（3）x轴上是否存在点P使△OPD为直角三角形，若存在，请直接写出P点的坐标。若不存在，请说明理由；